有効数字の扱い方 part-3
前回に引き続き、有効数字の運用について解説していく。
有効数字と誤差(平均値の平均2乗誤差)
- 誤差の有効数字は原則1桁で表す。
- 但し、先頭の数字が1の場合2桁で記述する。
ここで例を挙げると、ある量$x$を測定して平均値$1.2345$と誤差(平均値の平均2乗誤差)$0.0246$を得たとする。

- 誤差の有効数字は原則1桁で表すので、小数第2位まで残すことになる。この例では$0.0246$の小数第2位まで残し、小数第3位を四捨五入し$0.02$とする。
- 「誤差は大きめに見積もる」という考えにより、小数第3位を四捨五入ではなく繰り上げて$0.03$と考える場合もある。担当の指導者に確認するとよい。
- 平均値は誤差の値と桁をそろえなければならないので平均値も小数第2位まで残すこととなる。小数第3位を四捨五入し、$1.23$とする。
- 計算結果は「$\text{真の値}= \text{平均値} \pm \text{誤差}$」の形で記述する。結果として$x=1.23 \pm 0.02$ と記述することになる。
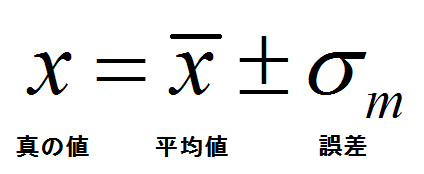

誤差の有効数字が1桁で無いケース
- 誤差の有効数字は原則1桁で記述するが、先頭の数字が1の場合2桁で記述する。
ある量を測定して平均値$1.2345$と誤差$0.0126$を得たとする。

誤差の先頭の数字が$1$なので、この場合は2桁分を記述することになる。よって、小数第3位まで残すことになり、小数第4位を四捨五入し、誤差は$0.013$とする。
平均値は誤差の桁とそろえるので、小数第4位を四捨五入して$1.235$とし、結果として$x = 1.235 \pm 0.013 $ と記述することになる。
測定器の精度と誤差
測定結果の誤差として用いる値は2つの候補がある。
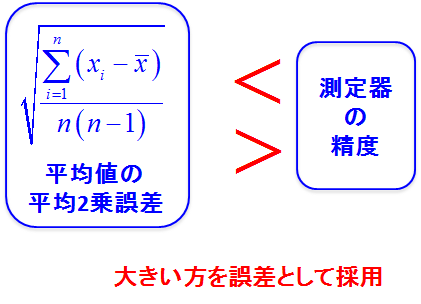
- 測定値の平均値の平均2乗誤差(ばらつき)による誤差
- 測定器の精度(測定器の図ることができる限界)による誤差
この2つの値を比べて大きい方を誤差として採用する。
よくある間違い例
デジタル天秤(精度 $0.1 \ \mbox{g}$)を用いて質量$m$を3回測定し、次の値を得たとする。
$$
\begin{array}{cc}
\hline
\text{質量}\ m & \mbox{[g]} \\
\hline
100.1 & \\
100.1 & \\
100.1 & \\
\hline
\end{array}
$$
平均値は$(100.1+100.1+100.1)/3 = 100.1 \ \mbox{g}$であり、誤差はばらつきがないので誤差$0$としてしまうケース
「誤差ゼロはありえない」という大原則を忘れない事。ばらつきが全くない場合は測定器の精度である$0.1 \ \mbox{g}$を誤差として使用することになる。
結果としては$m =( 100.1 \pm 0.1) \ \mbox{g}$とするのが正しい。
