力のモーメント ~ 練習問題 part-2
力のモーメントに関連した基礎的な練習問題を取り上げる。
円盤に力を加える
半径$L_1$と$L_2$の2つの円盤が接合されている。この円盤に下図のように力$F_1, \ F_2$を加えた。力のモーメントを求めよ。
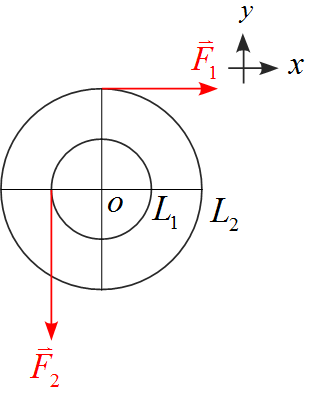
解答
下図の様に位置ベクトル$\vec{r}_1 ,\ \vec{r}_2$を設定する。
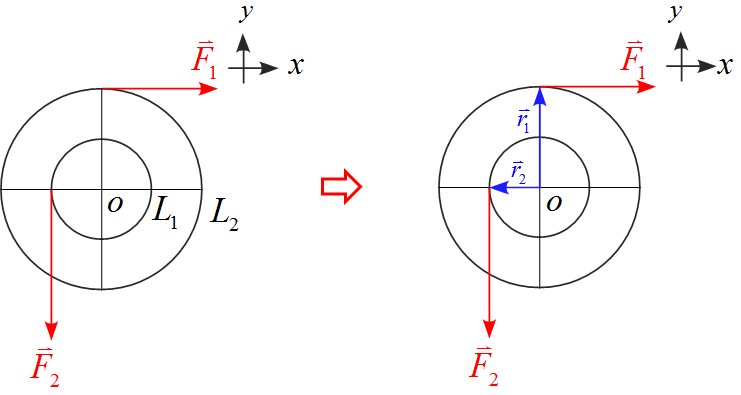
位置ベクトル$\vec{r}_1 ,\ \vec{r}_2$は
\begin{eqnarray*}
\vec{r}_1 &=&
\begin{pmatrix}
0 \\
L_2 \\
0 \\
\end{pmatrix} ,\ \quad
\vec{r}_2 &=&
\begin{pmatrix}
-L_1 \\
0 \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}
である。
作用する力$\vec{F}$は
\begin{eqnarray*}
\vec{F}_1 &=&
\begin{pmatrix}
F_1 \\
0 \\
0 \\
\end{pmatrix} ,\ \quad
\vec{F}_2 &=&
\begin{pmatrix}
0 \\
-F_2 \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}
である。
教科書的計算
力のモーメント$\vec{M}$の大きさは
\begin{eqnarray*}
| \vec{M} | = |\vec{r}||\vec{F}| \sin \theta
\end{eqnarray*}
より
\begin{eqnarray*}
| \vec{M}_1 | &=& |\vec{r}_1||\vec{F}_1| \sin \theta \\
\\
&=& L_2 \cdot F_1 \sin (-90^{\circ}) \\
\\
&=& - L_2 F_1
\end{eqnarray*}
\begin{eqnarray*}
| \vec{M}_2 | &=& |\vec{r}_2||\vec{F}_2| \sin \theta \\
\\
&=& L_1 \cdot F_2 \sin (90^{\circ}) \\
\\
&=& L_1 F_2
\end{eqnarray*}
であるから
\begin{eqnarray*}
M = M_1 +M_2 = - L_2 F_1 + L_1 F_2
\end{eqnarray*}
である。
外積を使って計算
\begin{eqnarray*}
\vec{M}_1 = \vec{r}_1 \times \vec{F}_1 &=&
\begin{pmatrix}
0 \\
L_2 \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
F_1 \\
0 \\
0 \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
L_2 \cdot 0 - 0 \cdot 0 \\
0 \cdot F_1 -0 \cdot 0 \\
0 \cdot 0 - L_2 \cdot F_1 \\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
- L_2 F_1 \\
\end{pmatrix}
\end{eqnarray*}
\begin{eqnarray*}
\vec{M}_2 = \vec{r}_2 \times \vec{F}_2 &=&
\begin{pmatrix}
-L_1 \\
0 \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
0 \\
-F_2 \\
0 \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
0 \cdot 0 - 0 \cdot (-F_2) \\
0 \cdot (-F_2) - (-L_1) \cdot 0 \\
(-L_1) \cdot (-F_2) - 0 \cdot 0 \\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
L_1 F_2 \\
\end{pmatrix}
\end{eqnarray*}
従って
\begin{eqnarray*}
\vec{M} &=& \vec{M}_1 + \vec{M}_2 \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
-L_2 F_1 \\
\end{pmatrix} +
\begin{pmatrix}
0 \\
0 \\
L_1 F_2 \\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
L_1 F_2 - L_2 F_1 \\
\end{pmatrix} \\
\end{eqnarray*}
力のモーメントの大きさは
\begin{eqnarray*}
M = |\vec{M}| &=& \sqrt{0^2 + 0^2 + ( L_1 F_2 - L_2 F_1)^2} \\
\\
&=& L_1 F_2 - L_2 F_1
\end{eqnarray*}
となる。