位置ベクトル・変位ベクトル

位置ベクトル・変位ベクトル

位置を決める ~ 位置ベクトル

　物体の運動を考える場合、その物体がどこにあるのか(位置するか)は重要な情報である。
　ある3次元空間を考え、原点$O$と物体のある位置$P$を設定する。直交座標系で図に表すと、下図のようになる。

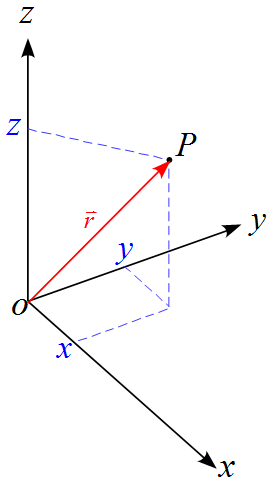
　ここで、原点$O$から物体の位置$P$までのベクトル$OP$ベクトルを位置ベクトルと呼ぶ。

\begin{eqnarray*}
\vec{r} =
\begin{pmatrix}
x \\
y \\
z \\
\end{pmatrix} \ , \ \ |\vec{r}| =\sqrt{x^2+y^2+z^2}
\end{eqnarray*}

位置ベクトルを単位ベクトルを使って表す

単位ベクトルとは

• 大きさが$1$で向きが決まっているベクトルのこと
• 直交座標系で$x,\ y,\ z$の軸に沿った単位ベクトルは大きさが$1$でそれぞれの軸の正の向きが単位ベクトルとなる。
• 単位ベクトルの大きさは$1$であるから、任意のベクトルの場合は自分自身の大きさで割れば単位ベクトルを表すことができる。

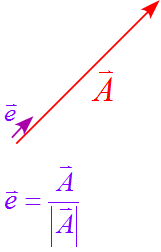
座標軸に沿った単位ベクトル

　単位ベクトルを使って表す

　$x,\ y,\ z\ $軸方向の単位ベクトルは下図のように$\vec{i}, \vec{j}, \vec{k}$や$\vec{e}_1, \vec{e}_2, \vec{e}_3$と表される。

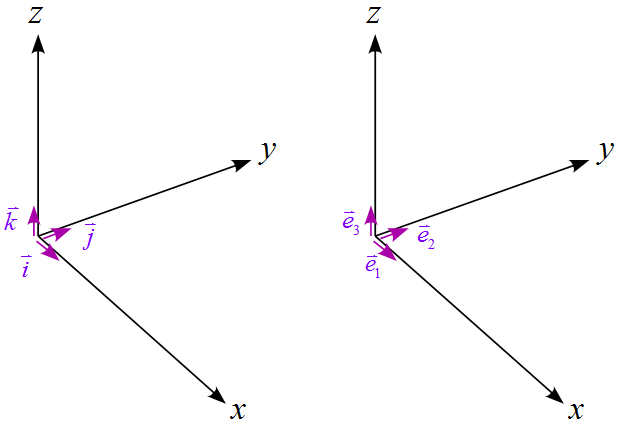
位置ベクトル$\vec{r}$を単位ベクトルを使って式で表すと

\begin{eqnarray*}
\vec{r} &=& x \vec{i} + y \vec{j} + z \vec{k} \\
\\
\vec{r} &=& x \vec{e}_1 + y \vec{e}_2 + z \vec{e}_3 \\
\end{eqnarray*}

と表される。

変位ベクトル ~ 物体の位置が動いたら

　ある運動によって物体が動いたとする。この時、物体がどれだけ動いたかを表している。
　ある空間を考え、原点$O$と物体のある位置$P$を設定する。ここで、点$P$から点$P'$に移動したとする。直交座標系で図に表すと下図のようになる。

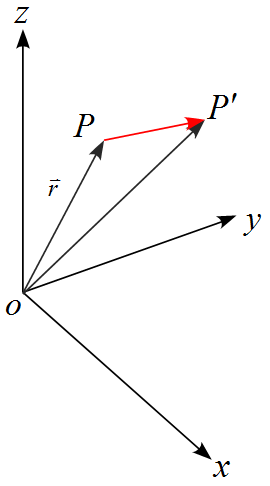
　点$P'$の位置ベクトルを$\vec{r}'$とすると、変位ベクトル$\Delta \vec{r}$は下図のようになり、

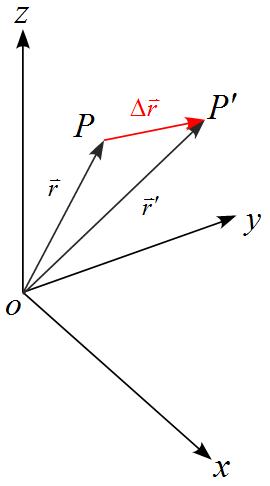
変位後のベクトルは

\begin{eqnarray*}
\vec{r}' = \vec{r} +\Delta \vec{r}
\end{eqnarray*}

と表される。$\Delta \vec{r} =(\Delta x,\ \Delta y, \ \Delta z)$とすると、

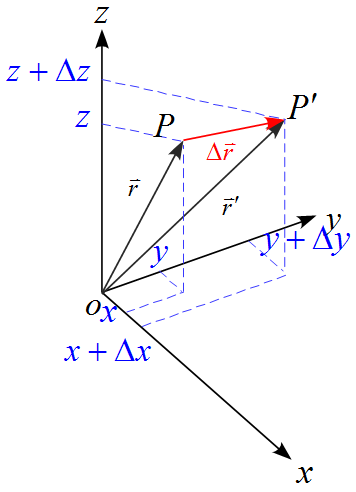
\begin{eqnarray*}
\vec{r}' &=& \vec{r} +\Delta \vec{r} \\
\\
\vec{r}' &=&
\begin{pmatrix}
x \\
y \\
z \\
\end{pmatrix} +
\begin{pmatrix}
\Delta x, \\
\Delta y \\
\Delta z \\
\end{pmatrix} =
\begin{pmatrix}
x + \Delta x \\
y + \Delta y \\
z + \Delta z\\
\end{pmatrix}
\end{eqnarray*}

　と表すことができる。これは各成分独立して考えることができることを表している。

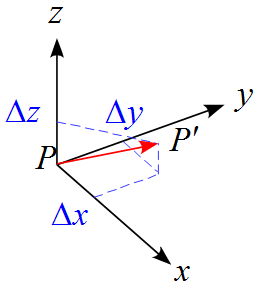
変位ベクトル ~ まとめ

　変位はベクトルであり、各成分ごとに独立して考えることができる。運動の種類によってそれぞれの軸に沿って考えればよい。

• 直線運動
  \begin{eqnarray*}
  x' = x + \Delta x
  \end{eqnarray*}
• 平面運動
  \begin{eqnarray*}
  x' &=& x + \Delta x \\
  \\
  y' &=& y + \Delta y
  \end{eqnarray*}
• 立体的な運動
  \begin{eqnarray*}
  x' &=& x + \Delta x \\
  \\
  y' &=& y + \Delta y \\
  \\
  z' &=& z + \Delta z
  \end{eqnarray*}