有効数字の扱い方 part-1

　測定を行う上では避けて通れない考え方の一つに「有効数字」というものがある。実験や数値計算を行う時に「有効数字を考えて計算せよ」と指導を受けていることであろう。「有効数字を扱う上でのルール」はいくつかあり、それを正しく理解することで正しい実験レポートが作成できる。
　ここでは有効数字の本質的な概念を理解し、運用できるようになることを目的に解説していく。

有効数字とは

意味のある数値のこと
具体的には「最後の位のみに誤差を含んでいる」という状態で表された数値のこと
有効数字は桁数で表す。

　例えば、物差しを使ってある長さを測定して$12.3\ \mbox{cm}$という値を得たとする。この値をうち、$1$と$2$の数字は確かに信頼できる数字である(読み間違えは除くが確実な数値であろう)。ここで、最後の数字を$3$と決定した時、即ち、目盛りを読んだ時、通常、物差しは$1\ \mbox{mm}$まで目盛りを振ってあるので$3$と読んだのは目分量で$2.5\ \mbox{mm}$よりは大きくて$3.5\ \mbox{mm}$よりは小さいので$3$と読み取った訳である。誤差として$0.5\ \mbox{mm}$つまり、$0.05\ \mbox{cm}$程度あるとは言え、$3$という数値はでたらめな値では無くそれなりに信頼できる値である。このように信頼できる値のことを有効数字と呼ぶ。

有効数字は桁数で表し、測定値の正確さの度合いを表す指標である。
今回の例では$1,\ 2,\ 3\ $が信頼できる値なので「有効数字$3$桁」と表現する。

　さて、ここで$12.3\ \mbox{cm}$という測定値を測定していない他人が見たとする。この測定値を見た人は「$3$に誤差があるんだな」と理解して数値を見ることになる。有効数字のルールは万国共通なので、知らない相手に測定値の確からしさを伝えるには重要なものである。

有効数字を考えた測定の仕方

　前出の例では$\mbox{mm}$までしか読み取らなかったが、一般的には「測定器の最小目盛りの$1/10$まで」を有効数字として用いる。つまり、$1 \ \mbox{mm}$の幅を目分量で読み取ることになる。デジタルの計測器で測定した場合には「測定可能の最小桁まで」を有効数字として用いる。

有効数字を考えた測定の原則

アナログの測定器の最小目盛りの$1/10$まで測定する
デジタルの測定器は測定可能の最小桁まで測定する

測定値を記述する上での注意

　測定した値を記述する場合には注意が必要である。例えば、測定した値が「$12.3 \ \mbox{cm}$」と記述する場合と「$12.30 \ \mbox{cm}$」と記述する場合とでは数値が示す意味が異なることになる。「$12.3 \ \mbox{cm}$」の場合には小数第1位に誤差を含んでいることを意味しているのに対し、「$12.30 \ \mbox{cm}$」の場合には$1, \ 2, \ 3 \ $の数字は確実で、小数第2位の$0$に誤差を含んでいることを意味している。それぞれ有効数字は「$12.3 \ \mbox{cm}$」の場合は3桁であり、「$12.30 \ \mbox{cm}$」の場合は4桁となる。測定の確からしさに違いが出てくるのである。

　従って、「最後の位の数値が$0$だからといって勝手に無いことにして書かなくて良いということにはならない」のである。

有効数字を扱う上でのポイント

　有効数字を扱う上でのポイントは3つある。

有効数字を考えた値は「最後の位のみに誤差を含んでいる」状態である。
有効数字の桁数を数えるとき、「位どりを表す$0$」は数えない。後ろの$0$は数える。
誤差の有効数字は原則1桁で表す。

　このルールを正しく運用するにはどうしたら良いかを考えながら計算することになる。有効数字と誤差の扱いについては次回に解説する。

有効数字と単位

「有効数字の桁数は単位を変えても変わらない」

　以下の具体例を参考に確認すると良い。

　$12.30 \times 10^{-2} \ \mbox{m}$と記述するのはよろしくない。計算途中の場合や表で桁をそろえたい場合を除いて、「$\mbox{1の位} \ . \ \mbox{小数点以下の値} \times 10^{n}$」の形で記述する。

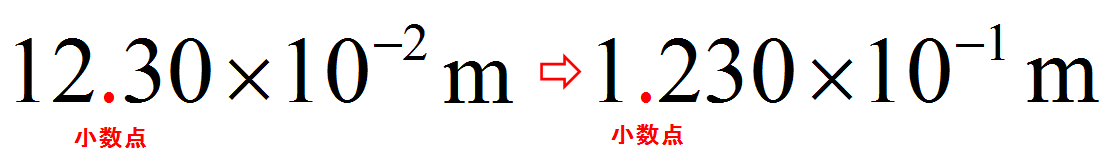
　接頭語の扱いについては別の機会で解説する。