有効数字の扱い方 part-2
前回に引き続き、有効数字の運用について解説していく。
有効数字を考慮した計算(物理的計算法)
- 「 最後の位のみに誤差を含んでいる」という状態で表す
この大原則を元に計算を行う。これを視覚的に確認するには筆算で表すとわかりやすい。
加減(和・差)
以下の計算例を参考に、誤差がどの範囲まで及ぶのか検討してみよう。
$1.23 +3.141$

- 単に数値を足した結果では、小数第2位と小数第3位に誤差を含んでいる状態となる。
- 誤差は最後の位にのみ含んでいる状態でなければならないので、小数第2位まで残すことになる。
- 小数第3位を四捨五入をし、$4.37$と記述する。有効数字は$3$桁でとなる。
$22.345 - 10.23$

- 単に数値を引いた結果では、小数第2位と小数第3位に誤差を含んでいる状態となる。
- 誤差は最後の位にのみ含んでいる状態でなければならないので、小数第2位まで残すことになる。
- 小数第3位を四捨五入をし、$12.12$と記述する。有効数字は$4$桁でとなる。
表現が悪いかもしれないが「誤差の汚染」がどうなっているか考えることが重要である。
有効数字 ~ 桁の増減
有効数字を考えて加減の計算を行った結果、有効数字の桁数が増えてしまう場合や有効数字の桁数が減ってしまう場合があり得ることを押さえておこう。
$2.46 + 8.62 $

- 有効数字3桁の値と有効数字3桁の値を足した結果、1の位が繰り上がり10の位までの値となっている。
- 誤差は最後の位にのみ含んでいる状態でなければならないので、小数第2位まで残すことになる。
- 結果として、有効数字が4桁に増えているが、原則通り(最後の位のみ誤差を含む)の形になっているので問題は無い。
$3.14 - 2.46 $
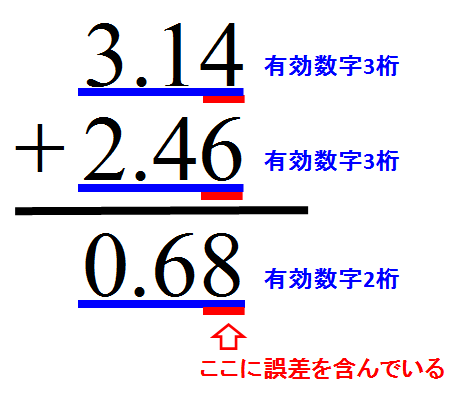
- 有効数字3桁の値と有効数字3桁の値を足した結果、1の位が繰り下がり小数点以下の値となっている。
- 誤差は最後の位にのみ含んでいる状態でなければならないので、小数第2位まで残すことになる。
- 結果として、有効数字が2桁に減っているが、原則通り(最後の位のみ誤差を含む)の形になっているので問題は無い。
乗除(積・商)
$1.23 \times 3.14 $

- 単に数値を掛けた結果では、小数第2位, 小数第3位, 小数第4位に誤差を含んでいる状態となる。
- 誤差は最後の位にのみ含んでいる状態でなければならないので、小数第2位まで残すことになる。
- 小数第3位を四捨五入をし、$3.86$と記述する。有効数字は$3$桁でとなる。
$1.234 \times 2.3 $
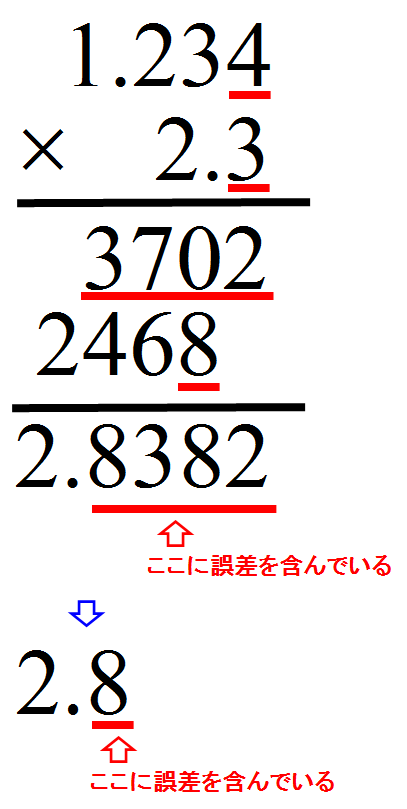
- 単に数値を掛けた結果では、小数第1位, 小数第2位, 小数第3位, 小数第4位に誤差を含んでいる状態となる。
- 誤差は最後の位にのみ含んでいる状態でなければならないので、小数第1位まで残すことになる。
- 小数第2位を四捨五入をし、$2.8$と記述する。有効数字は$2$桁でとなる。
$246 ÷ 135 $

- 割った結果の数値$1$と$8$は確実な値であるが、小数第2位の数値である$2$を決めるのに使った$300$は$3$からして誤差を含んでいるので、結果の$2$という値も誤差を含んでいると言える。
- 単に数値を割った結果では、小数第2位以下に誤差を含んでいる状態となる。(割り切れない)
- 誤差は最後の位にのみ含んでいる状態でなければならないので、小数第2位まで残すことになる。
- 小数第3位を四捨五入をし、$1.82$と記述する。有効数字は$3$桁でとなる。
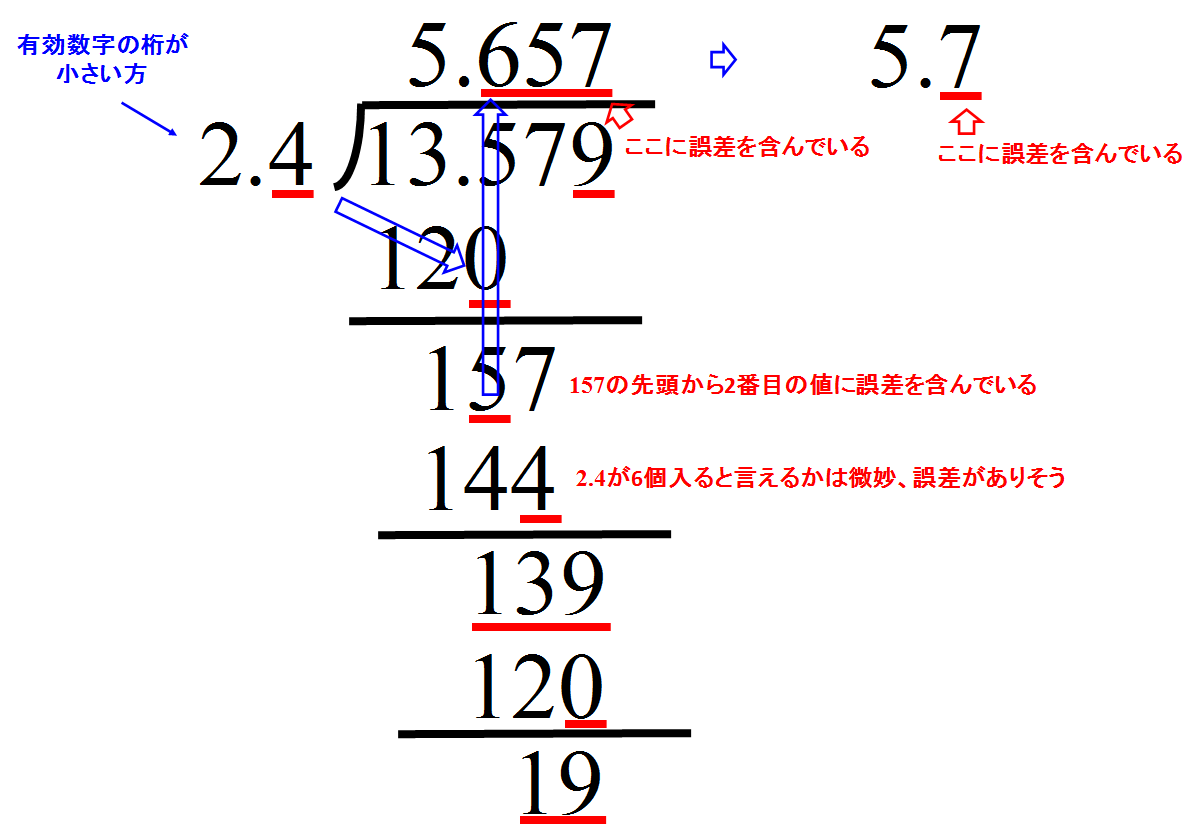
$13.579 ÷ 2.4 $

- 割った結果の数値$5$は確実な値であるが、小数第1位の数値である$6$を決めるのに使った$157$は先頭から2番めの値に誤差を含んでいるので、結果の$6$という値も誤差を含んでいると言える。
- 小数第2位の数値である$5$を決めるのに使った$139$は先頭の値からに誤差を含んでいるので、結果の$5$という値は大きく誤差を含んでいると言える。
- 単に数値を割った結果では、小数第1位以下に誤差を含んでいる状態となる。
- 誤差は最後の位にのみ含んでいる状態でなければならないので、小数第1位まで残すことになる。
- 小数第2位を四捨五入をし、$5.7$と記述する。有効数字は$2$桁でとなる。
$2.4 ÷ 1.3579 $

- 割った結果の数値$1$は確実な値であるが、小数第1位の数値である$7$を決めるのに使った$10421$は先頭から2番めの値から誤差を含んでいるので、結果の$7$という値も誤差を含んでいると言える。
- 小数第2位の数値である$6$を決めるのに使った$9157$は先頭の値からに誤差を含んでいるので、結果の$6$という値は大きく誤差を含んでいると言える。
- 単に数値を割った結果では、小数第1位以下に誤差を含んでいる状態となる。
- 誤差は最後の位にのみ含んでいる状態でなければならないので、小数第1位まで残すことになる。
- 小数第2位を四捨五入をし、$5.7$と記述する。有効数字は$2$桁でとなる。
有効数字を考慮した計算(物理的計算法)まとめ
- 加減の場合は「数値の最小の位の桁が大きいもの」に依る
- 乗除の場合は「有効数字の桁数の小さい方」に依る
- 「 最後の位のみに誤差を含んでいる」という状態で表す
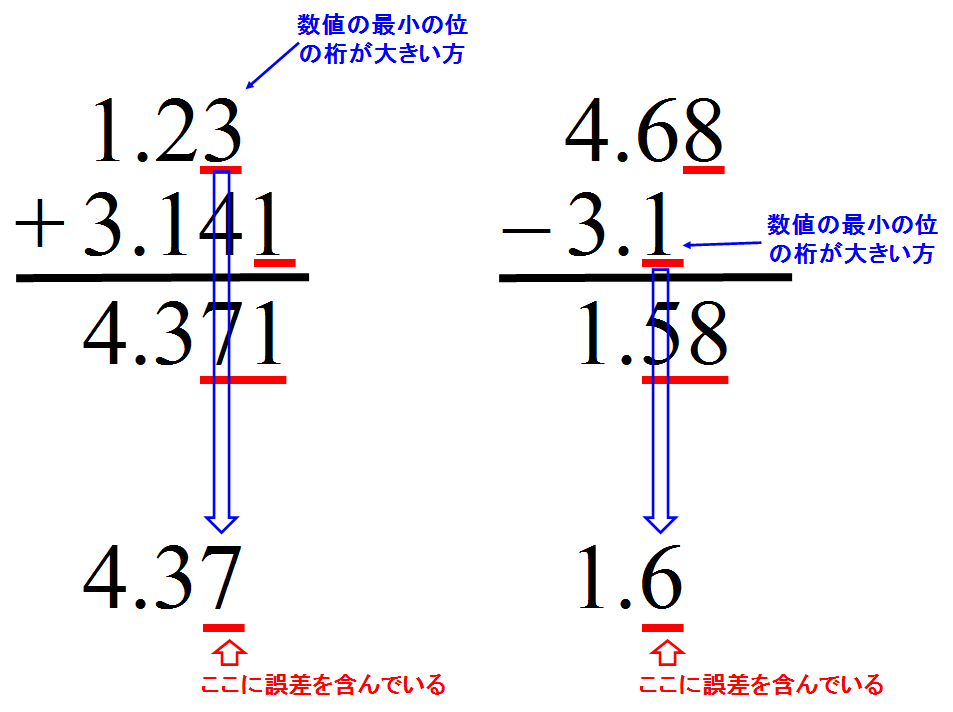
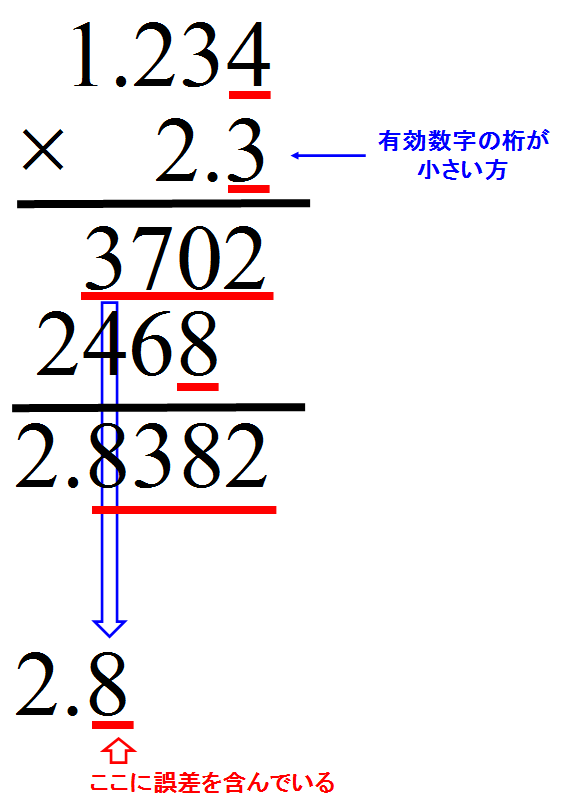

- 誤差は最後の位のみ含む状態で記述する。
- 計算途中の場合は1桁余分に書いてもよいが、最後で正しく処理をすること