運動方程式を立てるには作図が重要であることは前回に述べた通りである。今回も引き続き物理モデルを解説していく。
接触面から受ける力 ~ 抗力$R$
抗力$R$とは
- 物体に接触している面から受ける力を抗力$R$と呼ぶ。
- 抗力$R$の正体は電気的な力(分子間力)である。
- 分子一つ一つに作用する力を書き出すのは困難なので、全部をまとめて「抗力$R$」で表している。
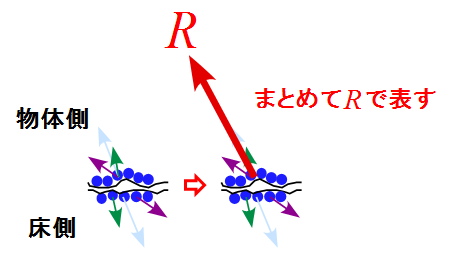
- 「抗力$R$が左右のどちらに傾くか?」は接触面に対して水平方向から受ける力によって変化する。
- 左側から力が作用した場合は、左に傾き、右側から力が作用した場合は右に傾く。
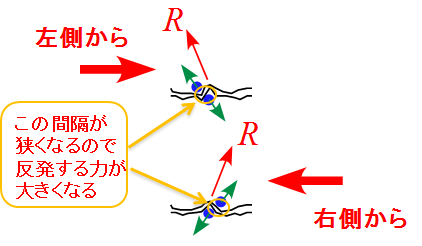
- 通常は抗力$R$の矢印1本で表し、下図のようになる。
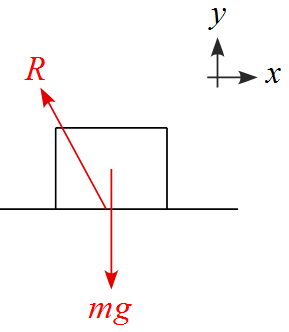
- 抗力$R$は下図のように、水平方向($x$方向)と垂直方向($y$軸方向)に分解することができる。
- 水平方向の成分を摩擦力$f$と呼び、垂直方向の成分を垂直抗力$N$と呼ぶ。
- 垂直抗力の$N$は「Normal component of reaction」の頭文字である。
- 抗力$R$と垂直抗力$N$とのなす角$\alpha$と設定する。
- 教科書や参考書等では予め垂直抗力$N$と摩擦力$f$が分解された状態での作図が多いが、面からの抗力$R$という概念が薄れてしまうので、抗力$R$の矢印を書き、それを分解した結果が垂直抗力$N$と摩擦力$f$という流れにした方が良い。
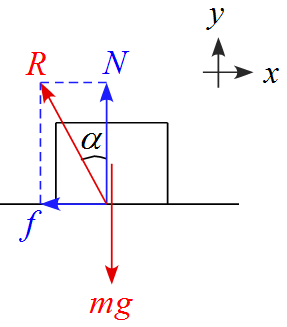
摩擦力$f$について
- 摩擦力$f$は面からの抗力$R$の水平方向成分である。
- 摩擦力$f$は運動している状態と静止している状態では異なる。
- 運動している状態の摩擦力を$f_k$と静止している状態の摩擦力を$f_s$とすると下図のような関係がある。
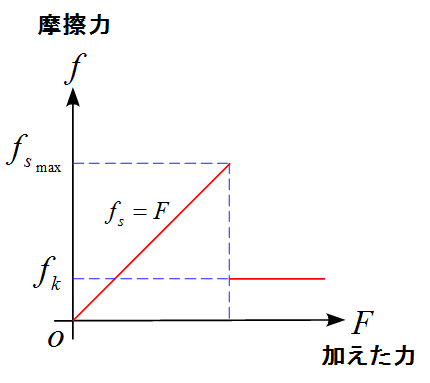
- 静止している物体に加えた力$F$が大きくなるにつれて摩擦力も大きくなるが、限界がある。静止している状態の摩擦力は$f_s=F$となる。限界を最大静止摩擦力$f_{s_\text{max}}$と呼ぶ
- 加えた力$F$が大きくなり限界を超えると物体は動き、運動する。この状態の摩擦力を動摩擦力$f_k$やすべり摩擦力と呼ぶ。
- 最大静止摩擦力$f_{s_\text{max}}$と動摩擦力$f_k$は$f_{s_\text{max}} > f_s$の関係である。力を加えていたら急にズルっと滑り出した実体験もあるだろう。
- 摩擦力$f$と垂直抗力$N$の比を摩擦係数$\mu$と定義し、最大静止摩擦力$f_{s_\text{max}}$については
\begin{eqnarray*}
\mu_s=\frac{f_{s_\text{max}}}{N} =\tan \alpha _s
\end{eqnarray*}であり、動摩擦力$f_k$については
\begin{eqnarray*}
\mu_k=\frac{f_k}{N} =\tan \alpha _k
\end{eqnarray*}の関係がある。
高校物理や大学初等物理の範囲内での説明でした。実は摩擦力というものは難しく奥が深いもので専門に研究されている研究室もあるくらいです。
荒い床(摩擦力のある)に置かれた物体を糸で引く
荒い床(摩擦力のある)に置かれた物体を糸で引くのモデル図
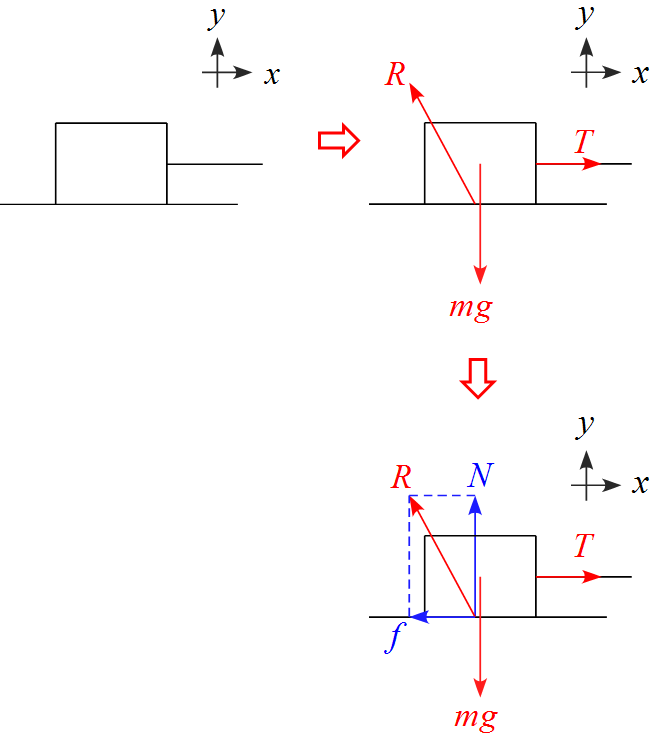
- $x$軸の正の向きは右側に、$y$軸の正の向きは上に設定した。
- 作用する力は重力$mg$, 引く力(張力)$T$, 接触面から受ける力(抗力) $R$ (Reaction) の3つである。
- 抗力を$x,\ y$軸に沿って分解すると垂直成分は「垂直抗力 $N$」、水平成分は「摩擦力 $f$」となる。
- 垂直抗力の$N$は「Normal component of reaction」の頭文字である。
荒い床(摩擦力のある)に置かれた物体を糸で引くの運動方程式
運動方程式は
\begin{eqnarray*}
m a_x &=& T-f \\
\\
m a_y &=& N-mg
\end{eqnarray*}
となる。
物体が静止している場合
物体が静止している状態では束縛条件より$a_x =0,\ a_y=0$となり
\begin{eqnarray*}
0 &=& T-f \\
\\
0&=& N-mg
\end{eqnarray*}
となる。
静止している状態では$T=f$であり、引く力$T$と摩擦力$f$は同じ大きさでつり合っていると言える。又、$N=mg$となり、垂直抗力$N$と重力$mg$の大きさが等しくなるが、これらの2つの力は「 作用・反作用の関係にない」ことに注意したい。
重力$mg$の源は万有引力であり、「地球が物体を引く力」である。従って、その反作用は「物体が地球を引く力」となる。
一方、垂直抗力$N$は接触面からの抗力$R$の垂直成分である。よって、「物体が面(床)から受ける力の垂直成分」なので、その反作用は「面(床)が物体から受ける力の垂直成分」となる。
物体が運動している場合
物体が床の上を動いている場合、束縛条件は$a_y=0$であり、
運動方程式は
\begin{eqnarray*}
m a_x &=& T-f \\
\\
0 &=& N-mg
\end{eqnarray*}
となる。
ここで、$f$は摩擦係数の定義 $\mu_k = \frac{f}{N} = \tan \alpha$より
\begin{eqnarray*}
f = \mu_k N
\end{eqnarray*}
と表されるので、
\begin{eqnarray*}
m a_x &=& T- \mu_k N \\
\\
m a_x &=& T- \mu_k mg
\end{eqnarray*}
となる。
床の上に物体が置かれている
床の上に物体が置かれているのモデル図
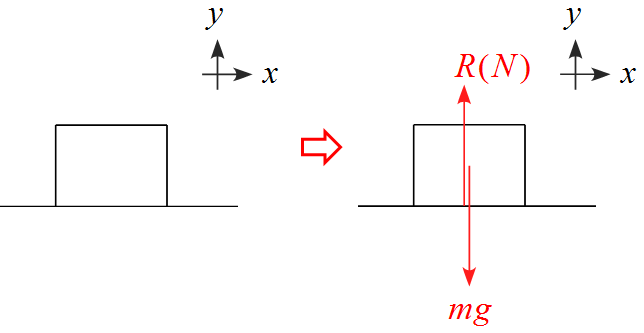
- $x$軸の正の向きは右側に、$y$軸の正の向きは上に設定した。
- 作用する力は重力$mg$, 接触面から受ける抗力$R$である。
- 水平方向に力は作用しないので接触面から受ける抗力$R$は垂直方向となす角$\alpha$はゼロになるので$R=N$である。
床の上に物体が置かれているの運動方程式
運動方程式は
\begin{eqnarray*}
m a_x &=0 \\
\\
m a_y &=& N-mg
\end{eqnarray*}
となる。
物体は静止しているので束縛条件は$a_x=0 ,\ a_y= 0$であり、
\begin{eqnarray*}
0 &=& N-mg
\end{eqnarray*}
となる。
斜面に置かれた物体の運動
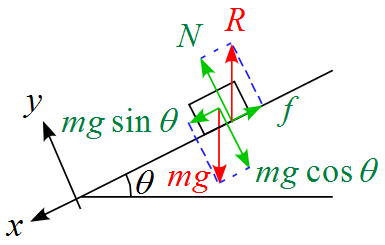
斜面に置かれた物体の運動のモデル図
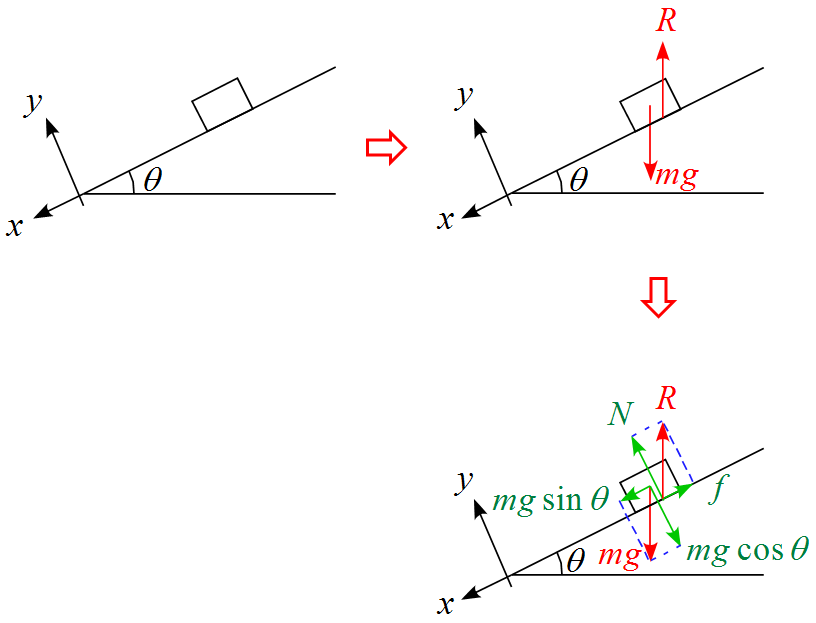
- $x$軸の正の向きは斜面に沿って下向きに、$y$軸の正の向きは斜面に垂直上向きに設定した。
- 作用する力は重力$mg$, 接触面から受ける力(抗力) $R$ (Reaction) の2つである。
- $x,y$軸に対して作用する力が斜めになっているので、軸に沿って成分を分解する。
- 抗力を$x,\ y$軸に沿って分解すると垂直成分は「垂直抗力 $N$」、水平成分は「摩擦力 $f$」となる。
- 重力$mg$を$x,\ y$軸に沿って分解すると垂直成分は「 $mg \cos \theta$」、水平成分は「$mg \sin \theta$」となる。
モデル図の悪い例
こんな図を書く人は居ないと思うかもしれないが、たまにこのような答案があるので困ってしまうところである。
重力$mg$が鉛直下向きではなく、斜めになった状態の図
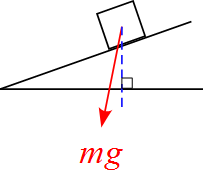
- 重力$mg$は鉛直下向きである。
- おそらく、抗力$R$の反作用と勘違いをして作図をしたと思われるが、抗力$R$は「斜面が物体を押す力」であり、その反作用は「物体が斜面を押す力」である。重力$mg$の反作用ではないことに注意する。
重力$mg$の斜面方向の成分$mg \sin \theta $の矢印が長すぎる図
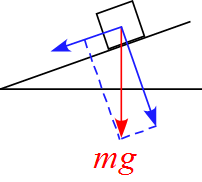
- おそらく重力$mg$を分解したものと理解していないことが原因と思われる。「$mg \sin \theta$ という力がある」ということだけ覚えていたと思われる。
- 重力$mg$を分解したと考えればありえない図ではある。
重力$mg$の分解が斜面沿ったに長方形ではない図
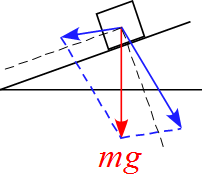
- 重力$mg$の分解としては間違ってはいない(ベクトルの分解としては)が、斜面(軸)に沿った形ではないので分解した意味がない。
- この図をもとにして運動方程式が立てられない。
矢印の長さが明らかにおかしい図
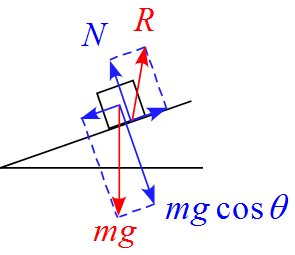
- 厳密に矢印の長さと力の大きさは一致している訳ではないが、ものすごく違和感を感じる。
- 多くのモデルで重力$mg$の垂直方向の成分$mg \cos \theta $と垂直抗力$N$は大きさが等しくなるので、矢印もそれに準ずる形で描く。厳密に長さを測って描くほどでは無いが、明らかに違うのはおかしい。
- 重力$mg$の斜面方向の成分$mg \sin \theta $と摩擦力$f$は運動している場合と、静止している場合に分けられる。静止しているならば矢印の長さは同じに、降っている場合は$mg \sin \theta $を長めに、上っている場合は摩擦力$f$を長めに描くと良い。
斜面に置かれた物体の運動の運動方程式
運動方程式は
\begin{eqnarray*}
m a_x &=& mg \sin \theta -f \\
\\
m a_y &=& N - mg \cos \theta
\end{eqnarray*}
となる。
束縛条件は$a_y =0$より、
\begin{eqnarray*}
m a_x &=& mg \sin \theta -f \\
\\
0 &=& N - mg \cos \theta
\end{eqnarray*}
となる。
物体が静止している場合
物体が静止している場合、$a_x =0$となり運動方程式は
\begin{eqnarray*}
0 &=& mg \sin \theta -f \\
\\
0 &=& N - mg \cos \theta
\end{eqnarray*}
となる。
物体が運動している場合
物体が運動している場合、動摩擦係数の定義 $\mu_k = \frac{f}{N}$ と運動方程式
\begin{eqnarray*}
m a_x &=& mg \sin \theta -f \\
\\
0 &=& N - mg \cos \theta
\end{eqnarray*}
より
\begin{eqnarray*}
m a_x &=& mg \sin \theta -\mu_k N\\
\\
m a_x &=& mg \sin \theta -\mu_k mg \cos \theta
\end{eqnarray*}
となる。
斜面に置かれた物体に水平方向から力$F$が作用する場合
斜面に置かれた物体に水平方向に左側から力$F$が作用した場合を考える。
斜面に置かれた物体に水平方向から力$F$が作用する場のモデル図
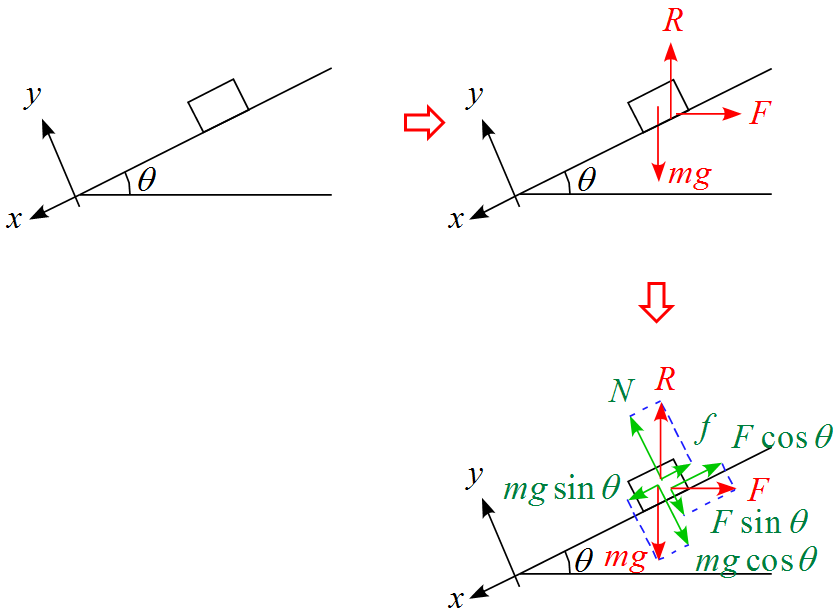
- $x$軸の正の向きは斜面に沿って下向きに、$y$軸の正の向きは斜面に垂直上向きに設定した。
- 作用する力は重力$mg$, 接触面から受ける力(抗力) $R$ (Reaction) , 水平方向の左側からに力$F$の3つである。
- 3つの作用する力は$x,y$軸に対して作用する力が斜めになっているので、軸に沿って成分を分解する。
- 抗力$R$を$x,\ y$軸に沿って分解すると垂直成分は「垂直抗力 $N$」、水平成分は「摩擦力 $f$」となる。
- 重力$mg$を$x,\ y$軸に沿って分解すると垂直成分は「 $mg \cos \theta$」、水平成分は「$mg \sin \theta$」となる。
- 水平方向の左側からに力$F$を$x,\ y$軸に沿って分解すると垂直成分は「 $F \sin \theta$」、水平成分は「$F \cos \theta$」となる。
斜面に置かれた物体に水平方向から力$F$が作用する場の運動方程式
運動方程式は
\begin{eqnarray*}
m a_x &=& mg \sin \theta -f - F \cos \theta \\
\\
m a_y &=& N - mg \cos \theta - F \sin \theta
\end{eqnarray*}
となる。
なめらかな斜面でかつ、静止している場合
なめらかな斜面でかつ、静止している場合の条件は$f =0, \ a_x=0, \ a_y=0 $であるから運動方程式は
\begin{eqnarray*}
0 &=& mg \sin \theta - F \cos \theta \\
\\
0 &=& N - mg \cos \theta - F \sin \theta
\end{eqnarray*}
となる。
従って、 水平方向の左側からに力$F$は
\begin{eqnarray*}
F \cos \theta &=& mg \sin \theta\\
\\
F &=& mg \frac{\sin \theta}{\cos \theta} =mg \tan \theta
\end{eqnarray*}
と表される。
また、垂直抗力$N$は
\begin{eqnarray*}
N &=& mg \cos \theta + F \sin \theta\\
\\
&=& mg \cos \theta + mg \frac{\sin \theta}{\cos \theta} \sin \theta\\
\\
&=& mg \left( \cos \theta + \frac{\sin ^2 \theta}{\cos \theta} \right) \\
\\
&=& mg \frac{\cos ^2 \theta + \sin ^2 \theta}{\cos \theta} \\
\\
&=& \frac{mg}{\cos \theta}
\end{eqnarray*}
と表される。