運動方程式を立てるには作図が重要であることは前回に述べた通りである。今回も引き続き物理モデルを解説していく。
慣性力
慣性力とは
これまでの運動は地上に固定された座標系において記述してきた。これを「慣性系」呼ぶ。(厳密に言うと地上は、即ち、地球は自転・公転をしているので近似的な慣性系と表現するのが妥当であろう。) ここでは、座標系自体がある加速度で移動しているような座標系を考える。このような座標系を「並進座標系」と呼ぶ。
下図のような2つの座標系を設定する。慣性系の座標軸を$x,y$軸とし、並進座標系の座標軸を$X,Y$軸とする。このとき、並進座標系は加速度$\vec{a}$で動いているとし、慣性系からみた物体の加速度を$\vec{\alpha}$, 並進座標系からみた物体の加速度を$\vec{\beta}$とする。
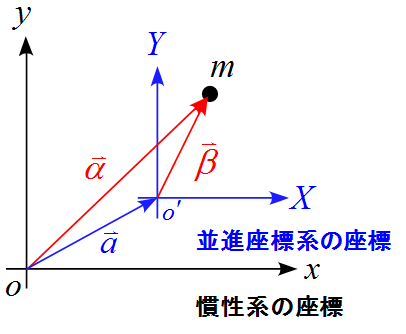
慣性系からみた物体の運動方程式は
\begin{eqnarray*}
m \vec{\alpha} = \vec{F}
\end{eqnarray*}
と記述できる。
ここで、加速度についてのベクトルの関係式より
\begin{eqnarray*}
\vec{\alpha} = \vec{a} + \vec{\beta}
\end{eqnarray*}
であるから運動方程式は
\begin{eqnarray*}
m \left( \vec{a} + \vec{\beta} \right) &=& \vec{F} \\
\\
m \vec{\beta} = \vec{F} - m \vec{a}
\end{eqnarray*}
と表される。
この式は、並進座標系から見た運動方程式を表していて、右辺の第2項$-m \vec{a}$を慣性力と呼ぶ。
このように考えると、並進座標系から見た場合、物体に働く力は実際に働いている力$\vec{F}$の他に見かけの力$-m \vec{a}$が観測されることになる。

並進座標系の加速度$\vec{a}$と逆向きに作用することを表している。
加速度$\alpha$で下降するエレベータ内に物体が糸でつるされている例
加速度$\alpha$で下降するエレベータ内に物体が糸でつるされている例のモデル図
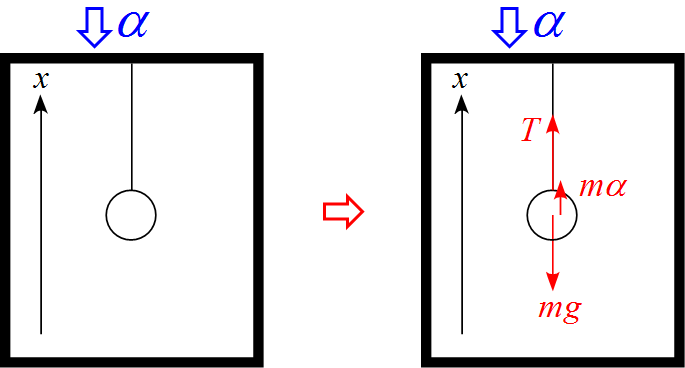
- エレベータ内に並進座標系を設定し、上向きを$x$軸の正とした。
- 作用する力は重力$mg$, 引く力(張力)$T$, 慣性力 $m \alpha$ の3つである。
- 慣性力 $m \alpha$はエレベータの進行方向逆向きである。
加速度$\alpha$で下降するエレベータ内に物体が糸でつるされている例の運動方程式
運動方程式は
\begin{eqnarray*}
ma = T - mg + m \alpha
\end{eqnarray*}
となる。
糸につるされた状態での束縛条件は$a = 0$ であり、
\begin{eqnarray*}
0 = T-mg + m \alpha
\end{eqnarray*}
となる。
\begin{eqnarray*}
T &=& mg - m \alpha \\
\\
T &=& m(g -\alpha)
\end{eqnarray*}
となり、$g - \alpha < 0 $となると糸がたるむことになる。
加速度$\alpha$で上昇するエレベータ内に物体が糸でつるされている例
加速度$\alpha$で上昇するエレベータ内に物体が糸でつるされている例のモデル図
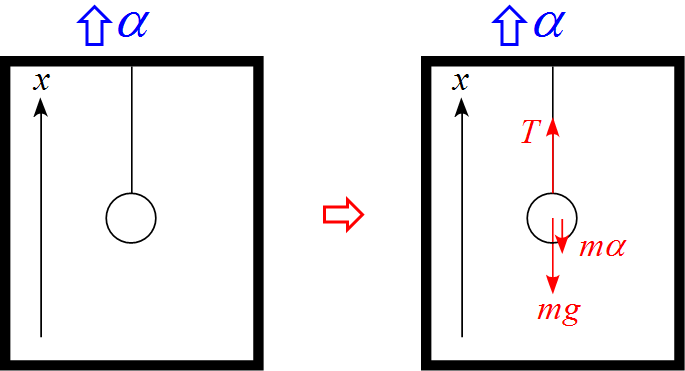
- エレベータ内に並進座標系を設定し、上向きを$x$軸の正とした。
- 作用する力は重力$mg$, 引く力(張力)$T$, 慣性力 $m \alpha$ の3つである。
- 慣性力 $m \alpha$はエレベータの進行方向逆向きである。
加速度$\alpha$で上昇するエレベータ内に物体が糸でつるされている例の運動方程式
運動方程式は
\begin{eqnarray*}
ma = T-mg -m \alpha
\end{eqnarray*}
となる。
糸につるされた状態での束縛条件は$a = 0$ であり、
\begin{eqnarray*}
0 = T-mg -m \alpha
\end{eqnarray*}
となる。
加速度$\alpha$で下降するエレベータ内の床に物体が置かれている例
加速度$\alpha$で下降するエレベータ内の床に物体が置かれている例のモデル図
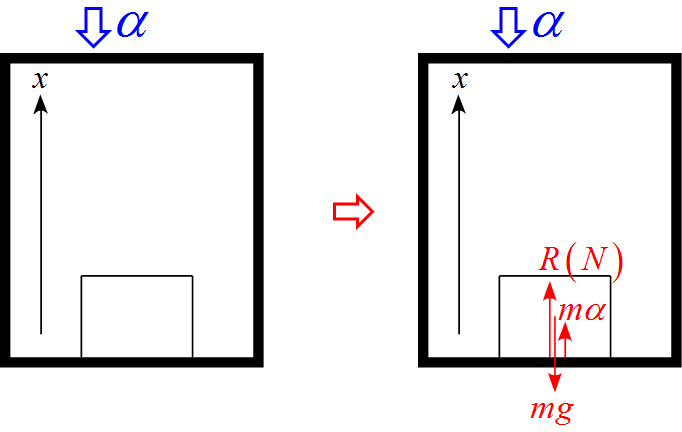
- エレベータ内に並進座標系を設定し、上向きを$x$軸の正とした。
- 作用する力は重力$mg$, 床からの抗力$R(N)$, 慣性力 $m \alpha$ の3つである。
- 慣性力 $m \alpha$はエレベータの進行方向逆向きである。
加速度$\alpha$で下降するエレベータ内の床に物体が置かれている例の運動方程式
運動方程式は
\begin{eqnarray*}
ma = N - mg + m \alpha
\end{eqnarray*}
となる。
床に置かれた状態での束縛条件は$a = 0$ であり、
\begin{eqnarray*}
0 = N - mg + m \alpha
\end{eqnarray*}
となる。
\begin{eqnarray*}
N &=& mg - m \alpha \\
\\
N &=& m(g -\alpha)
\end{eqnarray*}
となり、$g - \alpha < 0 $となると垂直抗力$N$が無くなり、無重量状態となる。
加速度$\alpha$で上昇するエレベータ内の床に物体が置かれている例
加速度$\alpha$で上昇するエレベータ内の床に物体が置かれている例のモデル図
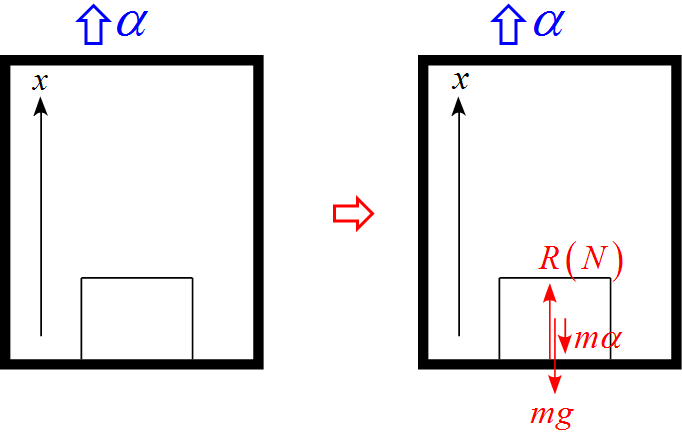
- エレベータ内に並進座標系を設定し、上向きを$x$軸の正とした。
- 作用する力は重力$mg$, 床からの抗力$R(N)$, 慣性力 $m \alpha$ の3つである。
- 慣性力 $m \alpha$はエレベータの進行方向逆向きである。
加速度$\alpha$で上昇するエレベータ内の床に物体が置かれている例の運動方程式
運動方程式は
\begin{eqnarray*}
ma = N - mg - m \alpha
\end{eqnarray*}
となる。
加速度$\alpha$で下降するエレベータ内での鉛直投げ上げ運動(初速度$v_0$)
加速度$\alpha$で下降するエレベータ内での鉛直投げ上げ運動のモデル図
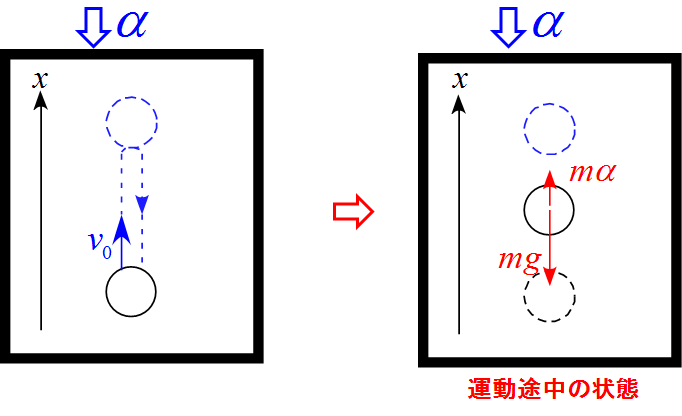
- エレベータ内に並進座標系を設定し、上向きを$x$軸の正とした。
- 作用する力は重力$mg$, 慣性力 $m \alpha$ の2つである。
- 慣性力 $m \alpha$はエレベータの進行方向逆向きである。
- 初速度$v_0$は作用する力とは関係ないことに注意する。
下降するエレベータ内での鉛直投げ上げ運動の運動方程式
運動方程式は
\begin{eqnarray*}
ma = -mg + m\alpha
\end{eqnarray*}
となる。
加速度$\alpha$で上昇するエレベータ内での鉛直投げ上げ運動(初速度$v_0$)
加速度$\alpha$で上昇するエレベータ内での鉛直投げ上げ運動のモデル図
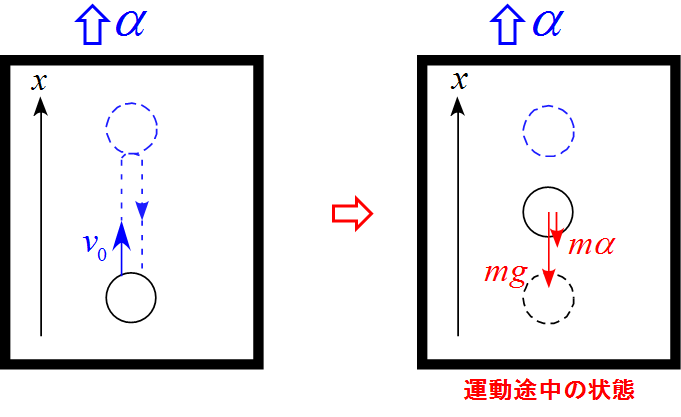
- エレベータ内に並進座標系を設定し、上向きを$x$軸の正とした。
- 作用する力は重力$mg$, 慣性力 $m \alpha$ の2つである。
- 慣性力 $m \alpha$はエレベータの進行方向逆向きである。
- 初速度$v_0$は作用する力とは関係ないことに注意する。
加速度$\alpha$で上昇するエレベータ内での鉛直投げ上げ運動の運動方程式
運動方程式は
\begin{eqnarray*}
ma = -mg - m \alpha
\end{eqnarray*}
となる。
水平方向に加速度$\alpha$で運動する列車
水平方向に加速度$\alpha$で運動する列車のモデル図
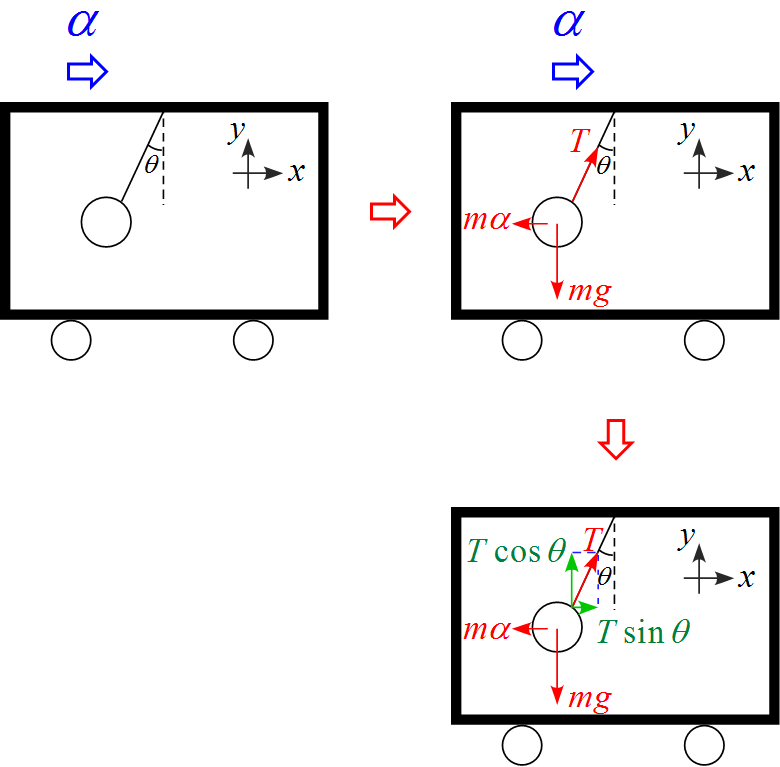
- エレベータ内に並進座標系を設定し、右向きを$x$軸の正とし、上向きを$y$軸の正とした。
- 作用する力は重力$mg$, 糸の張力$T$, 慣性力 $m \alpha$ の3つである。
- 慣性力 $m \alpha$はエレベータの進行方向逆向きである。
- 張力$T$を$x,\ y$軸に沿って分解すると垂直成分は「$T \cos \theta $」、水平成分は「$T \sin \theta $」となる。
水平方向に加速度$\alpha$で運動する列車の運動方程式
運動方程式は
\begin{eqnarray*}
m a_x &=& T \sin \theta - m \alpha \\
\\
m a_y &=& T \cos \theta -mg
\end{eqnarray*}
となる。
鉛直線とのなす角$\theta$を保った状態での束縛条件は$a_x = 0,\ a_y =0$ であり、
\begin{eqnarray*}
0 &=& T \sin \theta - m \alpha \\
\\
0 &=& T \cos \theta -mg
\end{eqnarray*}
となる。
従って、なす角$\theta$は
\begin{eqnarray*}
T \sin \theta &=& m \alpha \\
\\
T \cos \theta &=& mg\\
\\
\tan \theta &=& \frac{T \sin \theta}{T \cos \theta} = \frac{m \alpha}{mg} = \frac{\alpha}{g}
\end{eqnarray*}
と表される。