仕事とエネルギー ~ 練習問題 part-3
荒い水平面上の運動
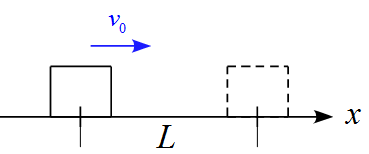
荒い水平面上を動く質量$m$の物体を考える。この物体に初速度$v_0$与えたところ距離$L$だけ動いて止まった。この運動について検討せよ。
接触面との摩擦力$f$は一定のものとして考えよ。
解答
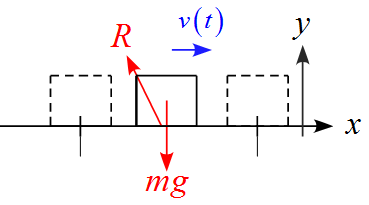
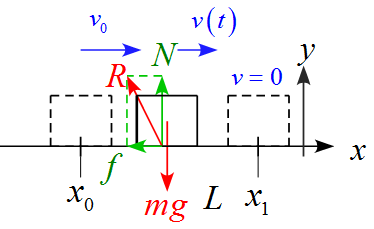
軸を設定し、作用する力を書き込む
- $x$軸の正の向きは右側に、$y$軸の正の向きは上に設定した。
- 作用する力は重力$mg ,\ $面からの抗力$R $ の2つである。
斜面に沿った成分に分解すると
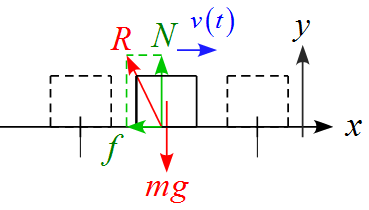
運動方程式を立てる
運動方程式は
\begin{eqnarray*}
ma_x &=& -f \\
\\
ma_y &=& N-mg
\end{eqnarray*}
となる。
仕事を計算する ~ 両辺を$x$で積分する
$x$軸の運動に着目するので$a_x = a$と書き換えて両辺を$x$で積分すると
\begin{eqnarray*}
ma &=& -f \\
\\
m \frac{\diff v}{\diff t} &=& (-f) \\
\\
\int m \frac{\diff v}{\diff t} \diff x &=& \int (-f) \diff x \\
\\
\int m \frac{\diff v}{\diff t} v \diff t &=& \int ( -f) \diff x \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t &=& \int (-f) \diff x \\
\end{eqnarray*}
となる。
ここで初期条件を$v(t_0) = v_0 ,\ v(t) = v ,\ x(t_0) = x_0 ,\ x(t) = x$とすると
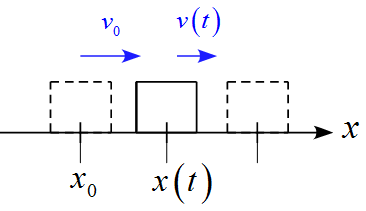
\begin{eqnarray*}
\int_{t_0}^{t} \frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t &=& \int_{x_0}^{x} (-f) \diff x \\
\\
\left[ \frac{1}{2} mv^2(t) \right]_{t_0}^{t} &=& [-fx]_{x_0}^{x} \\
\\
\frac{1}{2} mv^2(t) - \frac{1}{2} mv^2(t_0) &=& -fx - (-fx_0 ) \\
\\
\frac{1}{2} mv^2 - \frac{1}{2}mv_0^2 &=& -f(x - x_0) \\
\end{eqnarray*}
となる。

時刻$t_1$で物体が止まるとすると$v(t_1) =0 ,\ x(t_1) = x_1$であるから
\begin{eqnarray*}
\frac{1}{2} mv^2 - \frac{1}{2}mv_0^2 &=& -f(x - x_1) \\
\\
\frac{1}{2} m \cdot 0^2 - \frac{1}{2}mv_0^2 &=& -fL \\
\\
\frac{1}{2}mv_0^2 &=& fL
\end{eqnarray*}
となる。
物体に働く摩擦力$f$は
\begin{eqnarray*}
\frac{1}{2}mv_0^2 &=& fL \\
\\
f &=& \frac{1}{2} mv_0^2 \cdot \frac{1}{L} \\
\\
&=& \frac{mv_0^2}{2L}
\end{eqnarray*}
となる。
教科書的計算
運動方程式は
\begin{eqnarray*}
ma = -f
\end{eqnarray*}
となる。
摩擦力$f$は一定より、この運動は$a=\displaystyle -\frac{f}{m}= \text{const.}$の等加速度運動である。
等加速度運動の速度と距離の関係式の両辺に$\displaystyle \frac{1}{2}m$をかけると
\begin{eqnarray*}
v^2 - v_0^2 &=& 2ax \\
\\
\frac{1}{2} m \cdot v^2 - \frac{1}{2} m \cdot v_0^2 &=& \frac{1}{2} m \cdot 2ax \\
\\
\frac{1}{2} mv^2 - \frac{1}{2} mv_0^2 &=& max
\end{eqnarray*}
となる。運動方程式$ma=-f$より
\begin{eqnarray*}
\frac{1}{2} mv^2 - \frac{1}{2} mv_0^2 &=& -fx \\
\\
\frac{1}{2} mv^2(t) - \frac{1}{2} mv_0^2 &=& -fx \\
\end{eqnarray*}
となる。
初期条件$v(t_0) = v_0 ,\ v(t_1) =0 ,\ x_1-x_0 =L$より
\begin{eqnarray*}
\frac{1}{2} mv^2(t) - \frac{1}{2} mv_0^2 &=& -fx \\
\\
\frac{1}{2} m\cdot 0^2 - \frac{1}{2} mv_0^2 &=&-fL \\
\\
\frac{1}{2} mv_0^2 &=& f L \\
\end{eqnarray*}
となる。
物体に働く摩擦力$f$は
\begin{eqnarray*}
\frac{1}{2}mv_0^2 &=& fL \\
\\
f &=& \frac{1}{2} mv_0^2 \cdot \frac{1}{L} \\
\\
&=& \frac{mv_0^2}{2L}
\end{eqnarray*}
となる。