運動エネルギーと運動量
「運動エネルギー」も「運動量」もどちらも「運動の激しさ」を表した物理量である。2つの物理量の違いを確認しておこう。
運動エネルギーと仕事の関係
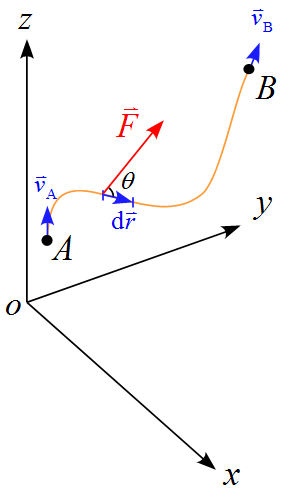
運動エネルギーと仕事の関係 ~ 両辺に$\diff \vec{r}$の内積を取って積分する
\begin{eqnarray*}
m\frac{\diff \vec{v}}{\diff t} &=& \vec{F} \\
\\
\int m\frac{\diff \vec{v}}{\diff t} \cdot \diff \vec{r} &=& \int \vec{F} \cdot \diff \vec{r} \\
\\
\int m\frac{\diff \vec{v}}{\diff t} \cdot \vec{v} \diff \vec{t} &=& \int \vec{F} \cdot \diff \vec{r} \\
\\
\int m \frac{\diff}{\diff t} \left( \frac{v^2}{2} \right) \diff \vec{t} &=& \int \vec{F} \cdot \diff \vec{r} \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff \vec{t}&=& \int \vec{F} \cdot \diff \vec{r}
\end{eqnarray*}

ここで、$\vec{v}(t_\text{A}) = v_\text{A}, \ \vec{v}(t_\text{B}) = v_\text{B}$とすると
\begin{eqnarray*}
\int_{t_\text{A}}^{t_\text{B}} \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff \vec{t}&=& \int_{\text{A}}^{\text{B}} \vec{F} \cdot \diff \vec{r} \\
\\
\frac{1}{2} m v^2 (t_\text{B}) - \frac{1}{2} m v^2 (t_\text{A}) &=& \int_{\text{A}}^{\text{B}} \vec{F} \cdot \diff \vec{r} \\
\\
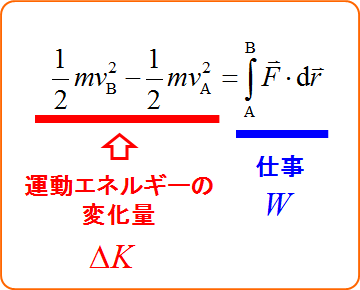
\frac{1}{2} m v_\text{B}^2 - \frac{1}{2} m v_\text{A}^2 &=& \int_{\text{A}}^{\text{B}} \vec{F} \cdot \diff \vec{r}
\end{eqnarray*}
となる。

運動量と力積の関係
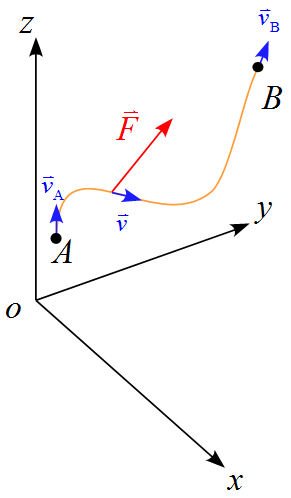
運動量と力積の関係 ~ 両辺を時間$t$で積分する
\begin{eqnarray*}
m \frac{\diff \vec{v}}{\diff t} &=& \vec{F} \\
\\
\int m \frac{\diff \vec{v}}{\diff t} \diff t &=& \int \vec{F} \diff t \\
\\
\int \frac{\diff}{\diff t} (m \vec{v}) \diff t&=& \int \vec{F} \diff t \\
\end{eqnarray*}
となる。
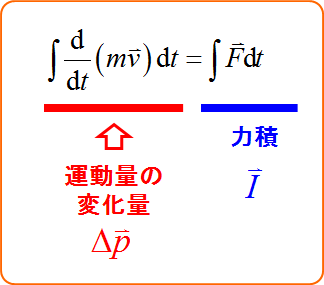
ここで、$\vec{v}(t_\text{A}) = v_\text{A}, \ \vec{v}(t_\text{B}) = v_\text{B}$とすると
\begin{eqnarray*}
\int_{t_{\text{A}}}^{t_{\text{B}}} \frac{\diff}{\diff t} (m \vec{v}) \diff t&=& \int_{t_{\text{A}}}^{t_{\text{B}}} \vec{F} \diff t \\
\\
[m\vec{v}(t)]_{t_{\text{A}}}^{t_{\text{B}}} &=& \int_{t_{\text{A}}}^{t_{\text{B}}} \vec{F} \diff t \\
\\
m \vec{v}(t_{\text{B}}) - m\vec{v}(t_{\text{A}}) &=& \int_{t_{\text{A}}}^{t_{\text{B}}} \vec{F} \diff t \\
\\
m\vec{v}_{\text{B}} - m \vec{v}_{\text{A}}&=& \int_{t_{\text{A}}}^{t_{\text{B}}} \vec{F} \diff t \\
\end{eqnarray*}
となる。
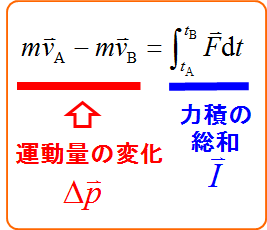

まとめ
「運動エネルギー」と「運動量」のいずれも「運動の激しさ」を表している。「運動エネルギーは距離的にどうか?」が問題であり、「運動量は時間的にどうか?」が問題となる。
- 運動方程式の「距離積分」 ~ 運動エネルギーと仕事の関係式
- 運動方程式の「時間積分」 ~ 運動量と力積の関係式