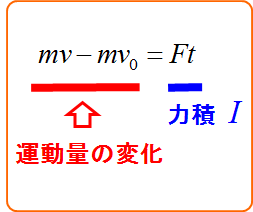
力積と運動量の関係
力積と運動量の関係
力積と運動量の関係を運動方程式から導く ~ 一般的な運動
質量$m$の質点が点$\text{A}$から点$\text{B}$まで力$\vec{F}$を受けて移動したとする。
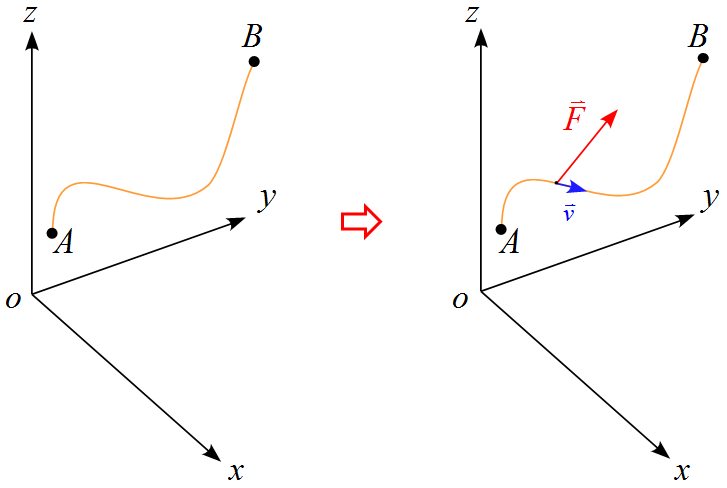
運動方程式は
\begin{eqnarray*}
m \frac{\diff \vec{v}}{\diff t} = \vec{F}
\end{eqnarray*}
となる。
この運動方程式において質量$m$が一定とすれば
\begin{eqnarray*}
\frac{\diff }{\diff t}(m\vec{v}) = \vec{F} \quad \ \cdots (*)
\end{eqnarray*}
と変形できる。
この式の形は「ニュートンが初めに提唱した運動方程式の形」である。$m\vec{a}=\vec{F}$が有名過ぎてあまり知られていないかもしれないがこちらが先である。
左辺の微分の中の部分である$m\vec{v}$を運動量$\vec{p}$と呼ぶ。運動エネルギーのときと同様に$\displaystyle \frac{\diff}{\diff t}(\quad \quad )$の内部の量は物理学的に意味のある量である。

運動量$\vec{p}$はベクトル量であることに注意したい。
さらに$m\vec{v}$を$\vec{p}$と置き換えると
\begin{eqnarray*}
\frac{\diff }{\diff t}(m\vec{v}) &=& \vec{F} \\
\\
\frac{\diff \vec{p}}{\diff t} &=& \vec{F} \\
\\
\diff \vec{p} &=& \vec{F}\diff t
\end{eqnarray*}
となる。
この式の左辺「$\vec{F}\diff t$」を「力積$\vec{I}$」と呼ぶ。
力積$\vec{I}$もベクトル量である。
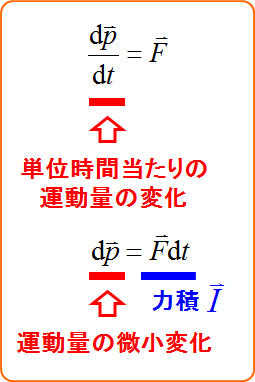
地点$\text{A}$と地点$\text{B}$の時刻をそれぞれ$t_{\text{A}}, \ t_{\text{B}}$とし、$v(t_{\text{A}})=v_{\text{A}} , \ v(t_{\text{B}})= v_{\text{B}}$として全区間積分すると
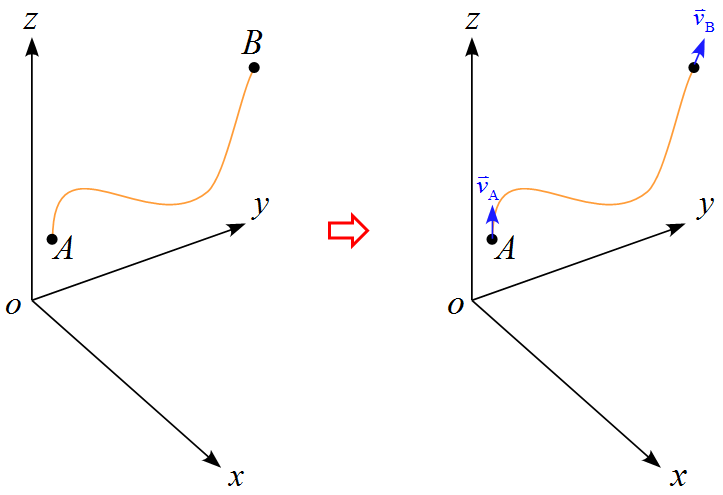
\begin{eqnarray*}
\diff \vec{p} &=& \vec{F}\diff t \\
\\
\int \diff \vec{p} &=&\int \vec{F}\diff t \\
\\
\int_{p_{\text{A}}}^{p_{\text{B}}} \diff \vec{p} &=&\int_{t_{\text{A}}}^{t_{\text{B}}} \vec{F}\diff t \\
\\
\vec{p}_{\text{A}} - \vec{p}_{\text{B}} &=& \int_{t_{\text{A}}}^{t_{\text{B}}} \vec{F}\diff t
\end{eqnarray*}
となる。
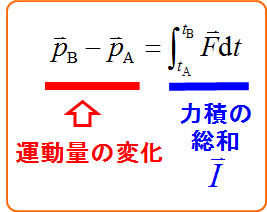
式(*)の左辺について
実際に計算すると
\begin{eqnarray*}
\frac{\diff }{\diff t}(m\vec{v}) = \frac{\diff m}{\diff t} \vec{v} + m \frac{\diff \vec{v}}{\diff t}
\end{eqnarray*}
となる。
ここで、質量が変化しない運動であれば$\displaystyle \frac{\diff m}{\diff t}=0$であるから
\begin{eqnarray*}
\frac{\diff }{\diff t}(m\vec{v}) = m \frac{\diff \vec{v}}{\diff t}
\end{eqnarray*}
であり、元の式となる。
運動方程式の両辺を$t$で積分する
運動方程式は
\begin{eqnarray*}
m \frac{\diff \vec{v}}{\diff t} = \vec{F}
\end{eqnarray*}
において、両辺を$t$で積分すると
\begin{eqnarray*}
m \frac{\diff \vec{v}}{\diff t} &=& \vec{F} \\
\\
\int m \frac{\diff \vec{v}}{\diff t} \diff t &=& \int \vec{F} \diff t \\
\\
\int \frac{\diff}{\diff t} (m \vec{v}) \diff t&=& \int \vec{F} \diff t \\
\\
[m\vec{v}]_{v(t_{\text{A}})}^{v(t_{\text{B}})} &=& \int \vec{F} \diff t \\
\\
m\vec{v}_{\text{B}} - m \vec{v}_{\text{A}}&=& \int \vec{F} \diff t \\
\end{eqnarray*}
となる。

教科書的計算
一般的な運動では運動方程式$ma=F$の両辺を$t$で積分を行った。運動の等加速度運動の場合を考える。
等加速度運動の速度は
\begin{eqnarray*}
v &=& v_0 +a t \\
\\
at &=& v-v_0 \\
\\
a &=& \frac{v-v_0}{t}
\end{eqnarray*}
となる。
運動方程式の両辺に$t$をかけると
\begin{eqnarray*}
ma &=& F \\
\\
ma \cdot t &=& F \cdot t \\
\\
m \frac{v-v_0}{t} t &=& Ft \\
\\
mv - mv_0 &=& Ft
\end{eqnarray*}
となり、「運動量の変化が力積に等しい」ことがわかる。