運動量と力積~ 練習問題 part-2
今回は運動量と力積に関連した基礎的な練習問題を取り上げる。
ボールを打ち返す
質量$m$のボールが右向きに速度$v_0$で飛んできたところ、真っ直ぐ左に打ち返した。打ち返したボールは速度$v_1$であったとするとボールが受けた力積$I$を求めよ。

解答
軸を設定し、作用する力を書き込む
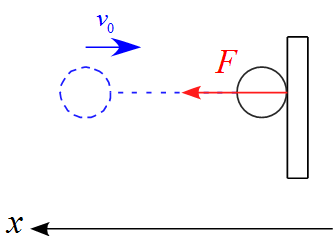
衝突した瞬間のモデル図は下図のようになる。
- $x$軸の正の向きは左側に設定した。
- 打ち返した力$F$の1つである。
運動方程式を立てる
衝突した瞬間の運動方程式は
\begin{eqnarray*}
ma = F
\end{eqnarray*}
となる。
力積を計算する ~ 両辺を$t$で積分する
\begin{eqnarray*}
ma &=& F \\
\\
m \frac{\diff v}{\diff t} &=& F \\
\\
\int m \frac{\diff v}{\diff t} \diff t &=&\int F \diff t\\
\\
\int \frac{\diff}{\diff t} (mv) \diff t &=& \int F \diff t
\end{eqnarray*}

初期条件を$v(t_0) = -v_0 ,\ v(t_1) = v_1 \ $とすると
\begin{eqnarray*}
\int \frac{\diff}{\diff t} (mv) \diff t &=& \int F \diff t \\
\\
\int_{t_0}^{t_1} \frac{\diff}{\diff t} (mv) \diff t &=& \int_{t_0}^{t_1} F \diff t \\
\\
[mv(t)]_{t_0}^{t_1} &=& \int_{t_0}^{t_1} F \diff t \\
\\
mv(t_1) - mv(t_0) &=& \int_{t_0}^{t_1} F \diff t \\
\\
mv_1 -m(-v_0) &=& \int_{t_0}^{t_1} F \diff t \\
\\
mv_1 + mv_0 &=& \int_{t_0}^{t_1} F \diff t \\
\end{eqnarray*}
となる。
従って、ボールが受けた力積$I$は
\begin{eqnarray*}
I =\int_{t_0}^{t_1} F \diff t = mv_1 + mv_0
\end{eqnarray*}
となる。
教科書的計算
運動量と力積の関係$\ mv' - mv = F \Delta t\ $より
\begin{eqnarray*}
mv(t_1) - mv(t_0) &=& F \Delta t \\
\\
mv_1 - m(-v_0) &=& F \Delta t \\
\\
mv_1 + mv_0 &=& F \Delta t
\end{eqnarray*}
となる。