仕事~ 練習問題 part-1
仕事に関連した基礎練習問題を取り上げる。
自由落下
質量$m$の物体が自由落下している。距離$L$だけ落下する際に重力のする仕事を求めよ。
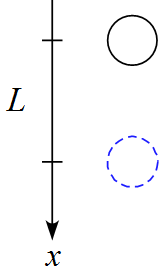
解答
下図のように、$x(t_0) = x_0 ,\ x(t_1) = x_1\ $と設定する。
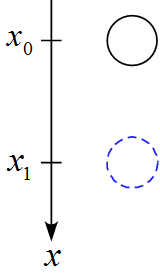
作用する力を書き込む
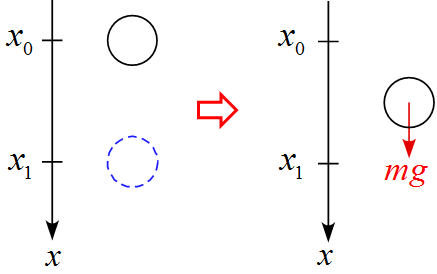
- 作用する力は重力$mg$のみである。
運動方程式を立てる
運動方程式は
\begin{eqnarray*}
ma &=& mg \\
\\
m\frac{\diff v}{\diff t} &=& mg
\end{eqnarray*}
となる。
仕事を求める
運動方程式の両辺を$x$で積分すると
\begin{eqnarray*}
m\frac{\diff v}{\diff t} &=& mg \\
\\
\int m\frac{\diff v}{\diff t} dx &=& \int mg dx \\
\\
\int m\frac{\diff v}{\diff t} v \diff t &=& \int mg dx \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t &=& \int mg dx \\
\end{eqnarray*}
となる。
ここで、$x(t_0) = x_0 ,\ x(t_1) = x_1\ $と設定したので
\begin{eqnarray*}
\int_{t_0}^{t_1} \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t &=& \int_{x_0}^{x_1} mg dx \\
\end{eqnarray*}
となる。
左辺が重力がする仕事$W_g$に相当するので
\begin{eqnarray*}
W_g &=& \int_{x_0}^{x_1} mg dx \\
\\
&=& \left[ mgx \right]_{x_0}^{x_1} \\
\\
&=& mgx_1 - mgx_0 \\
\\
&=& mg(x_1 - x_0)
\end{eqnarray*}
となる。問題では$x_1 - x_0=L$であるから
\begin{eqnarray*}
W_g =mgL
\end{eqnarray*}
となる。
教科書的計算
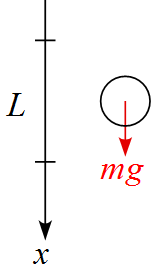
\begin{eqnarray*}
W_g &=& \text{力} \times \text{移動した距離} \\
\\
&=& mg \cdot L \\
\\
&=& mgL
\end{eqnarray*}
- 運動方程式は省略する事が多い。
- 下手すると、図すら書かない。
- 物理現象の全体像が薄れるデメリットが有る