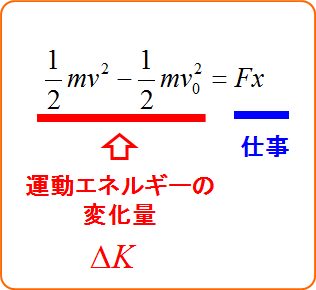
仕事とエネルギーの関係
エネルギーの話をする前に、先に仕事とエネルギーの関係について解説する。
仕事とエネルギーの関係を運動方程式から導く ~ 一般的な運動
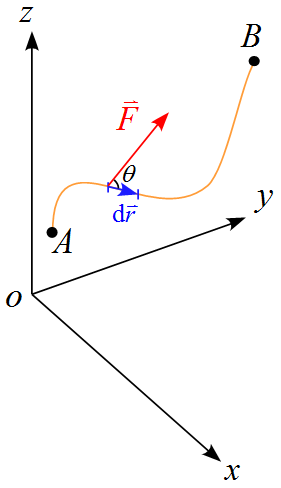
運動方程式は
\begin{eqnarray*}
m\frac{\diff \vec{v}}{\diff t} =\vec{F}
\end{eqnarray*}
である。微小区間の微小変位$\diff \vec{r}$を考える。
右辺を微小仕事となるように両辺に$\diff \vec{r}$の内積を取ると
\begin{eqnarray*}
m\frac{\diff \vec{v}}{\diff t} \cdot \diff \vec{r} =\vec{F} \cdot \diff \vec{r}
\end{eqnarray*}
と表すことができる。
点$\text{A}$から点$\text{B}$まで移動する間の仕事は全区間の積分することになるので
\begin{eqnarray*}
\int m\frac{\diff \vec{v}}{\diff t} \cdot \diff \vec{r} &=& \int \vec{F} \cdot \diff \vec{r} \\
\\
\int m\frac{\diff \vec{v}}{\diff t} \cdot \vec{v} \diff t &=& \int \vec{F} \cdot \diff \vec{r} \\
\\
\int m \frac{\diff}{\diff t} \left( \frac{v^2}{2} \right) \diff t &=& \int \vec{F} \cdot \diff \vec{r} \ \quad \cdots (*) \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t &=& \int \vec{F} \cdot \diff \vec{r}
\end{eqnarray*}
となる。
左辺の微分の中の部分「$\displaystyle \frac{1}{2}mv^2$」を「運動エネルギー$K$」と呼ぶ。物理学では時間変化を重視しているので、$\displaystyle \frac{\diff}{\diff t}\left( \quad \right) $の形に変形し、微分で括れた部分は意味のある量として扱うことが多い。
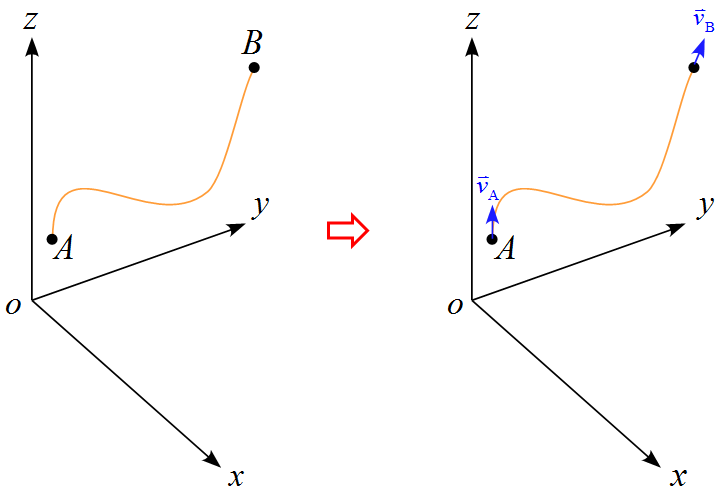
ここで、$\vec{v}(t_\text{A}) = v_\text{A}, \ \vec{v}(t_\text{B}) = v_\text{B}$とすると
\begin{eqnarray*}
\int_{t_\text{A}}^{t_\text{B}} \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t &=& \int_{\text{A}}^{\text{B}} \vec{F} \cdot \diff \vec{r} \\
\\
\left[ \frac{1}{2}mv^2(t) \right]_{t_\text{A}}^{t_\text{B}} &=& \int_{\text{A}}^{\text{B}} \vec{F} \cdot \diff \vec{r} \\
\\
\frac{1}{2} m v^2 (t_\text{B}) - \frac{1}{2} m v^2 (t_\text{A}) &=& \int_{\text{A}}^{\text{B}} \vec{F} \cdot \diff \vec{r} \\
\\
\frac{1}{2} m v_\text{B}^2 - \frac{1}{2} m v_\text{A}^2 &=& \int_{\text{A}}^{\text{B}} \vec{F} \cdot \diff \vec{r}
\end{eqnarray*}
となり、運動エネルギーの変化量$\Delta K$が仕事と等しいことがわかる。
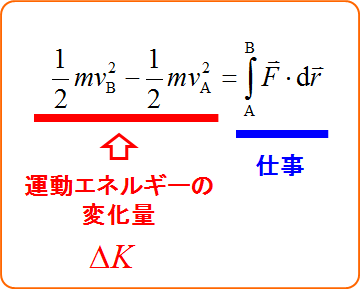
この関係式は「仕事とエネルギーの関係」を表している。
式$(*)$の左辺の導出について
左辺の$\displaystyle \frac{\diff \vec{v}}{\diff t} \cdot \vec{v}$の部分をつくるために
$\displaystyle \frac{\diff} {\diff t}(\vec{v}\cdot \vec{v})$を考える。
内積を計算すると
\begin{eqnarray*}
\frac{\diff} {\diff t}(\vec{v}\cdot \vec{v}) &=& \frac{\diff} {\diff t}(|\vec{v}|| \vec{v}| \cos \theta ) \\
\\
&=& \frac{\diff} {\diff t}(v \ v \ \cos 0 ) \\
\\
&=&\frac{\diff} {\diff t}(v^2)
\end{eqnarray*}
一方、展開すると
\begin{eqnarray*}
\frac{\diff}{\diff t}(\vec{v}\cdot \vec{v}) &=& \frac{\diff \vec{v}}{\diff t} \cdot \vec{v} + \vec{v} \cdot \frac{\diff \vec{v}}{\diff t} \\
\\
&=& 2 \frac{\diff \vec{v}}{\diff t} \cdot \vec{v}
\end{eqnarray*}
である。(内積のかける順は可換)
従って、
\begin{eqnarray*}
2 \frac{\diff \vec{v}}{\diff t} \cdot \vec{v} &=& \frac{\diff} {\diff t}(v^2) \\
\\
\frac{\diff \vec{v}}{\diff t} \cdot \vec{v} &=& \frac{\diff} {\diff t}(\frac{1}{2}v^2)
\end{eqnarray*}
となる。
仕事とエネルギーの関係を運動方程式から導く ~ 教科書的導出
- 運動のモデルは等加速度運動とする。
- 等加速度運動では作用する力$F$は一定である。
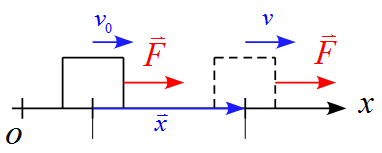
運動方程式は
\begin{eqnarray*}
ma = F
\end{eqnarray*}
及び、等加速度運動の速度と距離の関係式
\begin{eqnarray*}
v^2 - v_0^2 = 2ax
\end{eqnarray*}
を用いて導出する。
速度と距離の関係式の両辺に$\displaystyle \frac{1}{2}m$をかけ、式変形すると
\begin{eqnarray*}
v^2 - v_0^2 &=& 2ax \\
\\
\frac{1}{2} m \cdot v^2 - \frac{1}{2} m \cdot v_0^2 &=& \frac{1}{2}m \cdot 2ax \\
\\
\frac{1}{2} m v^2 - \frac{1}{2} m v_0^2 &=& max \\
\\
\frac{1}{2} m v^2 - \frac{1}{2} m v_0^2 &=& Fx \\
\\
\frac{1}{2} m v^2 - \frac{1}{2} m v_0^2 &=& W \\
\end{eqnarray*}
となり、運動エネルギーの変化量$\Delta K$が仕事$W$と等しいことがわかる。