仕事の定義
簡単なモデルとして、物体が$x$軸上を運動するとする。この運動で一定の力$\vec{F}$が作用して、物体を変位$\vec{x}$させたとする。
力$\vec{F}$が$x$軸上の場合
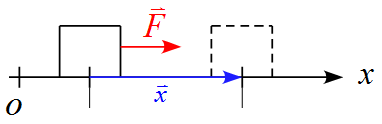
仕事$W$は
\begin{eqnarray*}
W &=& |\vec{F}| \cdot | \vec{x} | \\
\\
&=& Fx
\end{eqnarray*}
となる。仕事は英語の「work」の頭文字で表すことが多い。
力$\vec{F}$が$x$軸となす角$\theta$の場合
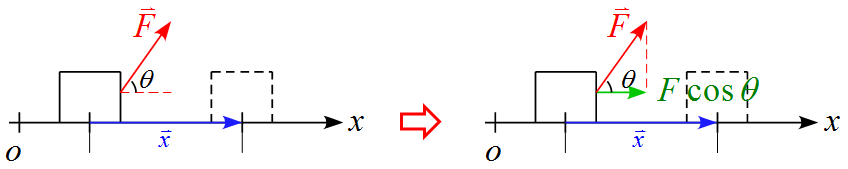
力$\vec{F}$が$x$軸となす角$\theta$の場合、変位に沿った力は$F\cos \theta$であるから
\begin{eqnarray*}
W &=& |\vec{F}| \cos \theta \cdot | \vec{x} | \\
\\
&=& F \cos \theta \cdot x \\
\\
&=& F x \cos \theta
\end{eqnarray*}
となる。
1つの式で表す
上記の2つの式を1つの式で表すと
\begin{eqnarray*}
W = \vec{F} \cdot \vec{x}
\end{eqnarray*}
となる。
ベクトルの内積を用いて表せばうまく表すことができる。
\begin{eqnarray*}
W &=& \vec{F} \cdot \vec{x} \\
\\
&=& |\vec{F}| | \vec{x} | \cos \theta
\end{eqnarray*}
である。
この式の有用なことは、仕事の正負はなす角$\theta$で決まるところである。変位$\vec{x}$と力$\vec{F}$のなす角が$0^{\circ}$から$90^{\circ}$の間は$\cos \theta$の値は正であり、$90^{\circ}$から$270^{\circ}$までの間は$\cos \theta$の値は負であり、
$270^{\circ}$から$360^{\circ}$までの間$\cos \theta$の値が正となる。
従って、「負の仕事はどうだったか?」とか悩むことはなく、変位$\vec{x}$と力$\vec{F}$のなす角だけ着目すれば良いことになる。
仕事の次元
仕事の次元は、定義 $W= \vec{F}\cdot \vec{x}$より
\begin{eqnarray*}
\text{仕事の次元} = [M]\frac{[L]}{[T^2]}[L] =\frac{[ML^2]}{[T^2]}
\end{eqnarray*}
と表される。
MKS単位系で単位を表すと
\begin{eqnarray*}
\text{仕事の単位} = [\mbox{J}] = [\mbox{Nm}] = [ \mbox{kg m/s}^2 \cdot \mbox{m} ] = [ \mbox{kg m}^2 \mbox{/s}^2 ]
\end{eqnarray*}
となる。
仕事の定義の一般化
前出の例は特殊な条件で考えたが、これを一般的なモデルに拡張する。
- 力$\vec{F}$が一定ではない
- 運動の軌道は一直線ではない
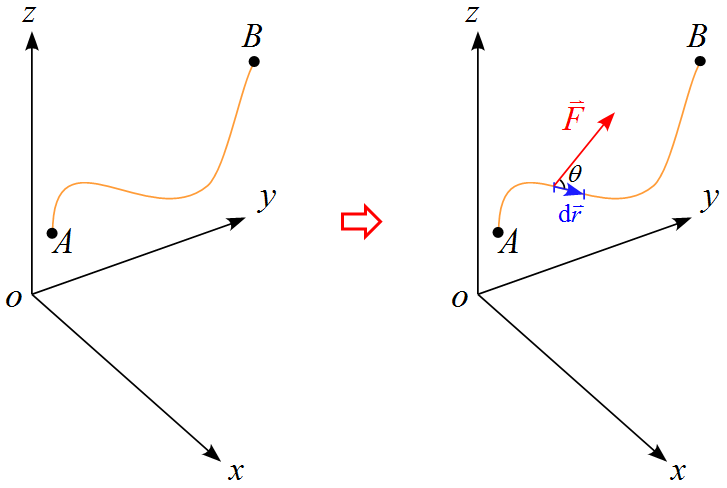
点$\text{A}$から点$\text{B}$までの間のある微小区間の微小仕事$\diff W$を考える。微小区間は直線で力Fも一定とみなせるので
\begin{eqnarray*}
\diff W &=& F \cos \theta \ \diff r \\
\\
&=& \vec{F} \cdot \diff \vec{r}
\end{eqnarray*}
これを最初から最後まで積分をすればよく
\begin{eqnarray*}
W = \int_c \vec{F} \cdot \diff \vec{r}
\end{eqnarray*}
となる。$c$は軌道に沿った線であり、このような積分を「線積分」と呼ぶ。
「微小部分を考えて積分する」という手法は物理ではよく使う方法です。
まとめ
力$\vec{F}$が一定で、直線運動の場合
\begin{eqnarray*}
W = \vec{F} \cdot \vec{x}
\end{eqnarray*}
となる。
一般的な運動の仕事は
\begin{eqnarray*}
W = \int_c \vec{F} \cdot \diff \vec{r}
\end{eqnarray*}
となる。
変位$\diff \vec{r}$と力$\vec{F}$は
\begin{eqnarray*}
\diff \vec{r} &=&
\begin{pmatrix}
\diff x \\
\diff y \\
\diff z \\
\end{pmatrix} ,\ \quad
\vec{F} &=&
\begin{pmatrix}
F_x \\
F_y \\
F_z \\
\end{pmatrix} \\
\end{eqnarray*}
とする。