力積の定義
運動方程式から力積を考える
\begin{eqnarray*}
m \vec{a} &=& \vec{F} \\
\\
m \frac{\diff \vec{v}}{\diff t} &=& \vec{F} \\
\\
\frac{\diff}{\diff t} \left( m \vec{v} \right) &=& \vec{F}\\
\\
\diff (m \vec{v}) &=& \vec{F} \diff t
\end{eqnarray*}
この右辺が微小な力積に相当し、全区間積分すると
\begin{eqnarray*}
\int \diff (m \vec{v}) &=&\int \vec{F} \diff t
\end{eqnarray*}
となる。

これを$F-t$グラフで表すと下図のようになる。
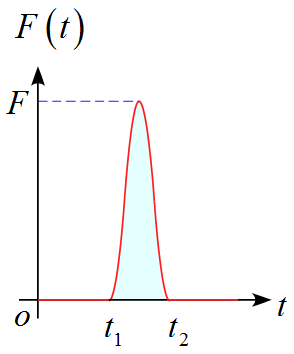
積分部分は水色で塗られた部分の面積に相当する。この面積は一般的には求めることが困難であるため、力積$I$を求めるの場合は運動量の変化から計算することになる。
$F$が一定とした場合
下図のように$F$の大きさが一定である場合は簡単に面積を計算することができる。
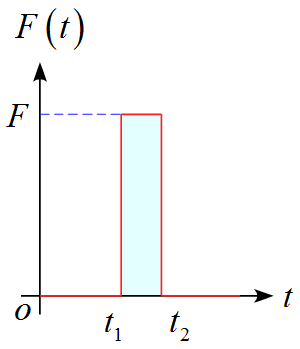
\begin{eqnarray*}
I &=& \int \vec{F} \diff t \\
\\
&=& \int_{t_1}^{t_2} F \diff t \\
\\
&=& F \cdot (t_2 - t_1)
\end{eqnarray*}
となる。
また、平均の力$\bar{F}$がわかる場合も同様に計算できる。
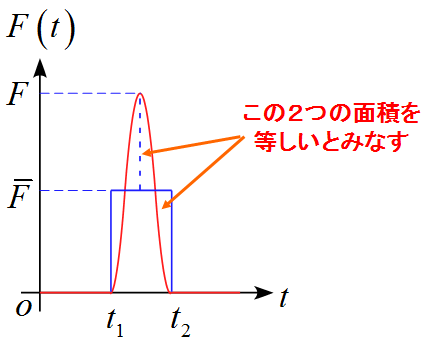
\begin{eqnarray*}
I &=& \int \vec{F} \diff t \\
\\
&=& \int_{t_1}^{t_2} \overline{F} \diff t \\
\\
&=& [\overline{F} t]_{t_1}^{t_2} \\
\\
&=& \overline{F}(t_2 - t_1) \\
\\
\end{eqnarray*}
となる。
力積の次元
力積の次元は、定義 $I=\int \vec{F} \diff t$より
\begin{eqnarray*}
\text{力積の次元} = \frac{[ML]}{[T^2]}[T] =\frac{[ML]}{[T]}
\end{eqnarray*}
と表される。
MKS単位系で単位を表すと
\begin{eqnarray*}
\text{力積の単位} = [\mbox{N s}] =[ \mbox{kg m/s}^2 \cdot \mbox{s} ] = [ \mbox{kg m} \mbox{/s} ]
\end{eqnarray*}
となる。