速度 (velocity)の定義

速度 (velocity)の定義

速度は直接には測れない

　車のスピードメータや投手の球速など、普段の生活で物体の速度(速さ)について触れる機会は多いと思う。これらの測定は速度を直接には測っていないことを理解しているだろうか？
物の長さや時間は測定器で直接測ることができる。物差しをあてたり、時計を読めば良いだろう。しかし、速度はそういう訳にはいかないのである。
　ここでは、速度について定義から解説していく。

速度の定義

　物体がある時刻$t$で点$\text{P}$の位置にあり、時刻$t + \Delta t $で点$\text{P}$にあったとする。つまり、時間$\Delta t$の間に$\Delta \vec{r}$変位したとする。

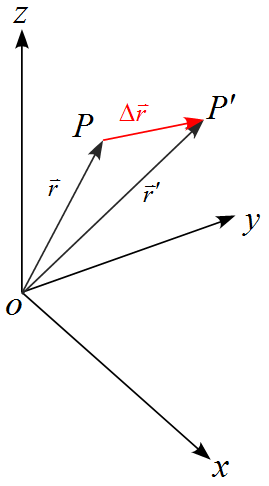
単位時間あたりの変位(時間に対する変位の変化率)は

\begin{eqnarray*}
\frac{\Delta \vec{r}}{\Delta t} &=& \frac{\vec{r}' - \vec{r}}{\Delta t} = \frac{\vec{r}(t+\Delta t) - \vec{r}(t)}{\Delta t} = \text{平均の速度}
\end{eqnarray*}

ここで$\Delta t =0$の極限を考えると

\begin{eqnarray*}
\lim_{\Delta t \to 0} \frac{\Delta \vec{r}}{\Delta t} = \lim_{\Delta t \to 0} \frac{\vec{r}(t+\Delta t) - \vec{r}(t)}{\Delta t} = \frac{\diff \vec{r}}{\diff t}
\end{eqnarray*}

これを速度$\vec{v}$と定義する。

速度 (velocity)と速さ (speed)

　普段の生活では速度と速さの区別を気にして使用していないかもしれないが、物理では明確に区別をして使用する。

• 速度：ベクトル量であり、大きさと向きを持つ量である。
• 速さ：スカラー量であり、大きさのみの量である。

速度 (velocity)のまとめ

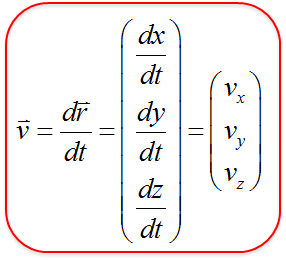
速度の場合も$x,\ y,\ z$成分ごとに独立して考えることができる。