等加速度直線運動
加速度運動には様々な運動があるが、高校物理の力学の範囲で学習する中心は「等加速度直線運動」であると言えよう。文字通り、「加速度が等しい運動」かつ「直線運動」のことである。具体的な例は「自由落下」「鉛直投げ上げ」等がある。
ここで誤解して欲しくないが、一般的な運動は等加速度ではない。高校物理の題材として理解のしやすいシンプルなモデルとして学習しているのであり、特殊な例と思っていたほうが良い。世の中には簡単にモデル化できない事例もたくさんあるということを知っておこう。
今回はこの「等加速度直線運動」について解説していく。
等加速度直線運動は加速度の定義$a=\displaystyle \frac{\diff v}{\diff t}$より
\begin{eqnarray*}
a=\frac{\diff v}{\diff t} = a_0 \ \ \text{(一定)}
\end{eqnarray*}
と表される。
$a-t$グラフ
$a-t$グラフは
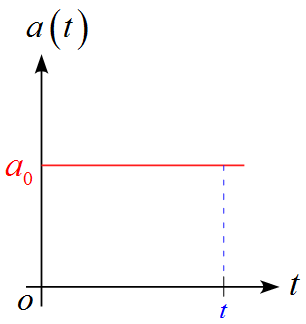
となる。
- 加速度$a$は常に$a_0$で一定である。
- $a(t)=a_0$と表される
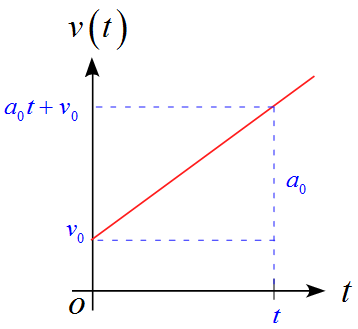
$v-t$グラフ
$v-t$グラフは
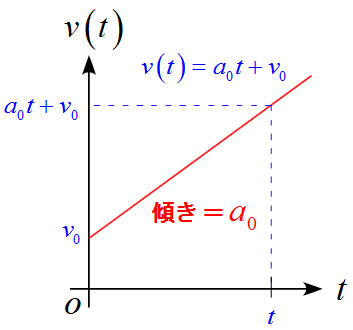
となる。
- 加速度の定義より、加速度は$v-t$グラフの傾きを表している。
- 傾きは一定値$a_0$である。
- $v(t)=a_0 t + v_0 $と表される。($v_0$は初速度)
- $v(t)$は変数が$t$である。
$x-t$グラフ
$x-t$グラフは

となる。
- 位置は$x(t)=\displaystyle \frac{1}{2} a_0 t^2 + v_0 t + x_0$と表される。($v_0$は初速度)
- 変位は$t$の2次関数である。
$a=\displaystyle \frac{\diff v}{\diff t}$を$t$で積分する
高校物理の範囲からは超えるが、数学の内容自体は高校数学の範囲である。
加速度$a_0=\text{一定}$として計算すると
\begin{eqnarray*}
\frac{\diff v}{\diff t} &=& a_0 \\
\\
\int \frac{\diff v}{\diff t} \diff t &=& \int a_0 \diff t \\
\\
\int \diff v &=& \int a_0 \diff t \\
\\
v &=& a_0 t+C \ \ \text{(C:積分定数)}
\end{eqnarray*}
となる。ここで、初期条件$v(0)=v_0$とすると
\begin{eqnarray*}
v(0) = a_0 \cdot 0+C &=& v_0 \\
\\
C &=& v_0
\end{eqnarray*}
となり、
\begin{eqnarray*}
v(t) = a_0 t +v_0
\end{eqnarray*}
となる。
この計算を$a-t$グラフで考えると、微小時間$\Delta t$の間の速度変化は$a_0 \Delta t$である。これを時刻$0 \to t$まで足し合わせる。即ち、$0$から$t$まで積分をすれば速度の変化分が計算できる。
さらに、初速度$v_0$を加えたものが、ある時刻$t$での速度を表していることになる。
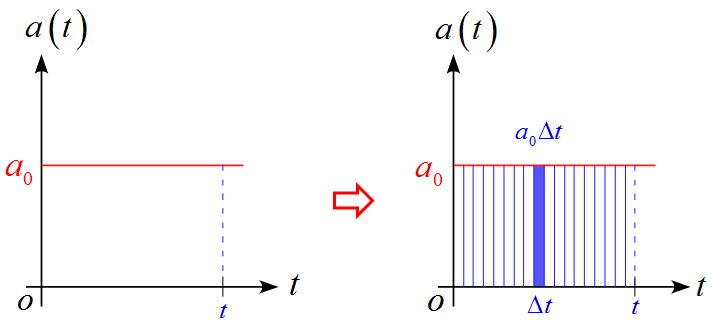
$v=\displaystyle \frac{\diff x}{\diff t}$を$t$で積分する
高校物理の範囲からは超えるが、数学の内容自体は高校数学の範囲である。
等加速度直線運動の速度を$v(t)=a_0 t+ v_0$として計算すると
\begin{eqnarray*}
\frac{\diff x}{\diff t} &=& a_0 t +v_0 \\
\\
\int \frac{\diff x}{\diff t} \diff t &=& \int (a_0 t +v_0) \diff t \\
\\
\int \diff x &=& \int (a_0 t +v_0) \diff t \\
\\
x &=& \frac{1}{2} a_0 t^2 +v_0 t +C' \ \ \text{(C':積分定数)}
\end{eqnarray*}
となる。ここで、初期条件$x(0)=x_0$とすると
\begin{eqnarray*}
x(0) = \frac{1}{2} a_0 \cdot 0^2+v_0 \cdot 0 +C' &=& x_0 \\
\\
C &=& x_0
\end{eqnarray*}
となり、
\begin{eqnarray*}
x(t) = \frac{1}{2} a_0 t^2 +v_0 t +x_0
\end{eqnarray*}
となる。
この計算を$v-t$グラフで考えると、時刻$t_n$から$t_n +\Delta t $の微小時間$\Delta t$間の変位は$(a_0 t_n +v_0) \Delta t$である。これを時刻$0 \to t$まで足し合わせる。即ち、$0$から$t$まで積分をすれば変位が計算できる。
さらに、初期位置$x_0$を加えたものが、ある時刻$t$での位置を表していることになる。
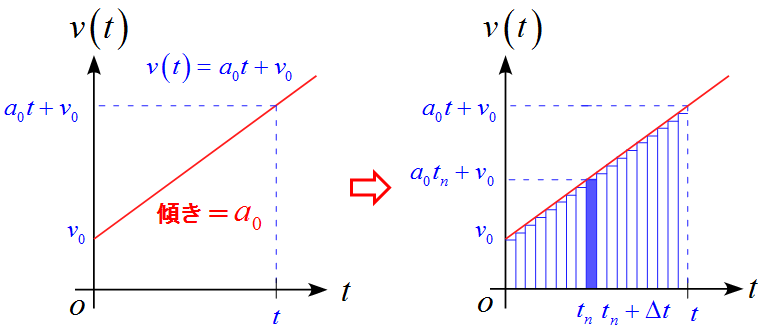
この求める面積は、実際には簡単に計算でき、下部分の長方形は$v_0 t$となり上部分の三角形は$\displaystyle \frac{1}{2}at^2$となる。
等加速度直線運動まとめ
- $v-t$グラフにおいて傾きが一定$a_0$である。
- 速度は$v(t) =a_0 t +v_0$ と表される。
- 変位は$x(t) =\displaystyle \frac{1}{2} a_0 t^2 +v_0 t$と表される。
- 位置は$x(t) =\displaystyle \frac{1}{2} a_0 t^2 +v_0 t +x_0$と表される。
- 変位と速度の式から$v^2 - v_{0}^2 =2a_0 x$とも表される。
- 注) 変位と位置の扱いには注意すること。原点基準($x_0 =0$)なら問題は無いが、問題文をよく読むこと。