加速度 ~ 練習問題 part-1
今回は加速度に関連した基礎的な練習問題を取り上げる。
平均の加速度$\bar{a}$
問題 1-1
自動車$\text{A}$は、$t = 0.0\ \mbox{s}$で動き始めて$4.0\ \mbox{s}$後に$12\ \mbox{m/s}$の速度になった。また、$4.0\ \mbox{s}$の速度で進んでいた自転車$\text{B}$は加速して$6.0\ \mbox{s}$後に$10.0\ \mbox{m/s}$の速度になった。
自動車$\text{A}$と自転車$\text{B}$の平均の加速度$\bar{a}$を求めよ。
- 自動車$\text{A}$ : 速度変化$\Delta v = (12-0)\ \mbox{m/s} =12 \ \mbox{m/s}$
- 自動車$\text{A}$ : 時間$\Delta t = (4.0 - 0.0)\ \mbox{s} = 4.0 \ \mbox{s}$
- 自転車$\text{B}$ : 速度変化$\Delta v = (10.0-4.0) \ \mbox{m/s} =6.0 \ \mbox{m/s}$
- 自転車$\text{B}$ : 時間$\Delta t = (6.0 - 0.0)\ \mbox{s} = 6.0 \ \mbox{s}$
自動車$\text{A}$の$v-t$グラフ
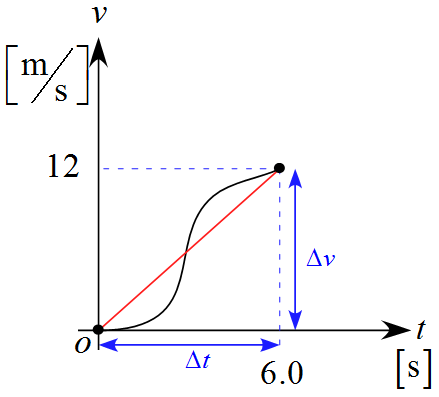
- 曲線部分は任意
自転車$\text{B}$の$v-t$グラフ
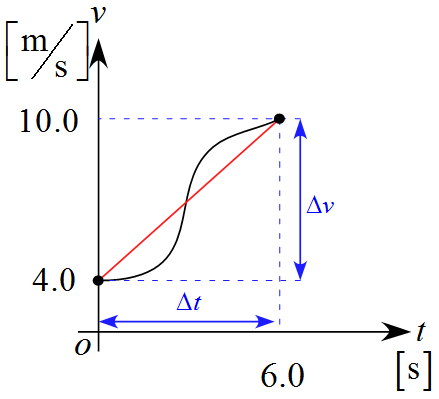
- 曲線部分は任意
数値計算
加速度の定義$a=\displaystyle \frac{\diff v}{\diff t}$より
\begin{eqnarray*}
\bar{a}_{\text{A}} &=& \frac{\Delta v}{\Delta t} \\
\\
&=& \frac{(12-0) \ \mbox{m/s}}{(4.0 - 0.0) \ \mbox{s}}=\frac{12 \ \mbox{m/s}}{4.0 \ \mbox{s}} =3.0 \ \mbox{m/s}^2
\\
\\
\bar{a}_{\text{B}} &=& \frac{\Delta v}{\Delta t} \\
\\
&=& \frac{(10.0-4.0) \ \mbox{m/s}}{(6.0 - 0.0) \ \mbox{s}}=\frac{6.0 \ \mbox{m/s}}{6.0 \ \mbox{s}} =1.0 \ \mbox{m/s}^2
\\
\end{eqnarray*}
となる。
- 頭の中イメージは$v-t$グラフ。できれば簡単にでも書き出すべき。
- 加速度の定義$a=\displaystyle \frac{\diff v}{\diff t}$から求める。
- 与えられた数値は有効数字2桁なので、結果も有効数字2桁で答える。小数点以下の$0$を勝手に省略しないこと。
問題 1-2
$x$軸上を直線運動する物体について考える。物体の速度が$v(1.0\ \mbox{s})=8.0\ \mbox{m/s}$であり、$v(3.0\ \mbox{s}) =2.0 \ \mbox{m/s}$であったとする。時刻$t=1.0\ \mbox{s}$から$3.0\ \mbox{s}$までの間の平均の加速度の大きさ$\bar{a}$及び向きを求めよ。
- 速度変化$\Delta v =( 2.0 -8.0) \ \mbox{m/s}=-6.0 \ \mbox{m/s}$
- 時間$\Delta t =( 3.0 - 1.0 ) \ \mbox{s}= 2.0 \ \mbox{s}$
$v-t$グラフ

- 曲線部分は任意
数値計算
加速度の定義$a=\displaystyle \frac{\diff v}{\diff t}$より
\begin{eqnarray*}
\bar{a}_{\text{A}} &=& \frac{\Delta v}{\Delta t} \\
\\
&=& \frac{(2.0-8.0) \ \mbox{m/s}}{(3.0 - 1.0) \ \mbox{s}}=\frac{-6.0 \ \mbox{m/s}}{2.0 \ \mbox{s}} =-3.0 \ \mbox{m/s}^2
\end{eqnarray*}
となる。
従って、加速度$\bar{a}$の大きさは$-3.0 \ \mbox{m/s}^2$ であり$x$軸の負の向きとなる。
- 頭の中イメージは$v-t$グラフ。できれば簡単にでも書き出すべき。
- $v-t$グラフを描けば傾きが負であることは確認できる。
- 加速度の定義$a=\displaystyle \frac{\diff v}{\diff t}$から求める。
- 与えられた数値は有効数字2桁なので、結果も有効数字2桁で答える。小数点以下の$0$を勝手に省略しないこと。