近似計算 物理基礎 (物基 315) 啓林館
$(1+x)^n \approx 1+na$
$|x|<<1$のとき、$x$の2次以上の項を無視することができ、 \begin{eqnarray*} (1+x)^n \approx 1+na \end{eqnarray*} となる。 これはテーラー展開(マクローリン展開)すれば確認することができる。
テーラー展開
\begin{eqnarray*}
f(x) &=& f(a) + f'(a) (x-a) + \frac{1}{2!} f"(a) (x-a)^2 + \cdots
&=& \sum _{n=0}^{\infty} \frac{1}{n!} f^{(n)} (a)(x-a)^n
\end{eqnarray*}
従って
\begin{eqnarray*}
(1+x)^n &=& 1+nx +\frac{1}{2} n(n-1) x^2 + \cdots\\
\\
&=& \sum _{n=0}^{\infty} \frac{n(n-1) \cdots (n-k+1)}{k!} x^k \ \ (|x| < 1)
\end{eqnarray*}
となる。
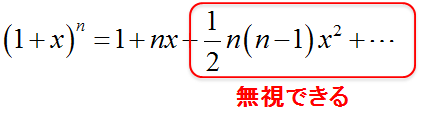
$\sin x \approx x,\ \cos x \approx 1$
$x <<1$のとき、2次以上の項を無視することができ \begin{eqnarray*} \sin x \approx x\\ \cos x \approx 1\\ \end{eqnarray*} となる。
テーラー展開
テーラー展開をすると、
\begin{eqnarray*}
f(x)=\sin x&= & 0+\frac{1}{1!}x+\frac{0}{2!}x^2+\frac{-1}{3!}x^3+\frac{0}{4!}x^4+\frac{1}{5!}x^5\cdots\\
\\
&=& x-\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots+\frac{(-1)^n}{(2n+1)!}x^{2n+1}+\cdots
\end{eqnarray*}
\begin{eqnarray*}
f(x)=\cos x&=& 1+\frac{0}{1!}x+\frac{-1}{2!}x^2+\frac{0}{3!}x^3+\frac{1}{4!}x^4+\frac{0}{5!}x^5\cdots\\
\\
&=& 1-\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots+\frac{(-1)^n}{(2n)!}x^{2n}+\cdots
\end{eqnarray*}
となる。
