運動量と力積~ 練習問題 part-6
今回は運動量と力積に関連した基礎的な練習問題を取り上げる。
軸上からの衝突
なめらかな水平面上で、物体$\text{A}$と物体$\text{B}$を衝突させる。物体$\text{A, B}$の質量は共に$m$である。
物体$\text{A}$の速度$\vec{v}_{A}=(6v, \ 0), \ $物体$\text{B}$の速度$\vec{v}_{B}=(0, \ 8v), \ $で衝突させたところ、衝突後の物体$\text{A}$の速度が$\vec{v}'_{A}=(2v, \ 5v)$となった。
(1) 物体$\text{B}$の衝突後の速度$\vec{v}'_{B}$を求めよ。
(2) 物体$\text{B}$に加わった力積$\vec{I}_{\text{B}}$を求めよ。

解答
軸を設定し、作用する力を書き込む
- $x$軸の正の向きは右側に、$y$軸の正の向きは上に設定した。
- 2物体が衝突する瞬間に受ける力は物体$\text{A}$が物体$\text{B}$から受ける力$\vec{F}_{\text{AB}}$と物体$\text{B}$が物体$\text{A}$から受ける力$\vec{F}_{\text{BA}}$の2つである。
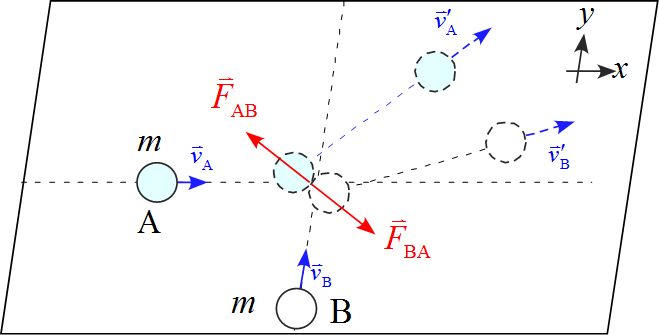
運動方程式は物体$\text{A}$について
\begin{eqnarray*}
m_{\text{A}} a_{\text{A}} &=& \vec{F}_{\text{AB}} \\
\\
m_{\text{A}} \frac{\diff \vec{v}_{\text{A}}}{\diff t} &=& \vec{F}_{\text{AB}} \\
\\
\frac{\diff}{\diff t} (m_{\text{A}} \vec{v}_{\text{A}}) &=& \vec{F}_{\text{AB}}
\end{eqnarray*}
となる。
運動方程式は物体$\text{B}$について
\begin{eqnarray*}
m_{\text{B}} a_{\text{B}} &=& \vec{F}_{\text{BA}} \\
\\
m_{\text{B}} \frac{\diff \vec{v}_{\text{B}}}{\diff t} &=& \vec{F}_{\text{BA}} \\
\\
\frac{\diff}{\diff t} (m_{\text{B}} \vec{v}_{\text{B}}) &=& \vec{F}_{\text{BA}}
\end{eqnarray*}
となる。
ここで、$\vec{F}_{\text{AB}}$と$\vec{F}_{\text{BA}}$は作用反作用の関係であるので、この力の大きさを$F$とおくと
\begin{eqnarray*}
\vec{F}_{\text{AB}} &=& \vec{F}
\\
\vec{F}_{\text{BA}} &=& -\vec{F}
\end{eqnarray*}
となるので
\begin{eqnarray*}
\frac{\diff}{\diff t} (m_{\text{A}} \vec{v}_{\text{A}}) &=& \vec{F}
\\
\frac{\diff}{\diff t} (m_{\text{B}} \vec{v}_{\text{B}}) &=& -\vec{F} \\
\\
\hline
\\
\frac{\diff}{\diff t} (m_{\text{A}} \vec{v}_{\text{A}}) + \frac{\diff}{\diff t} (m_{\text{B}} \vec{v}_{\text{B}}) &=& \vec{F} +(-\vec{F}) \\
\\
\frac{\diff}{\diff t} (m_{\text{A}} \vec{v}_{\text{A}} +m_{\text{B}} \vec{v}_{\text{B}} ) &=& \vec{0}
\end{eqnarray*}
となる。
となり、物体$\text{AB}$の衝突において運動量は保存していると言える。

従って、
\begin{eqnarray*}
m_{\text{A}} \vec{v}_{\text{A}} +m_{\text{B}} \vec{v}_{\text{B}} = m_{\text{A}} \vec{v}'_{\text{A}} +m_{\text{B}} \vec{v}'_{\text{B}}
\end{eqnarray*}
の関係式が導き出される。

運動量保存則を適用する
前述の通り、運動量保存則が成立することが確認できなので、これを適用していく。
問題の条件は
\begin{eqnarray*}
\vec{v}_{\text{A}}(t) &=&
\begin{pmatrix}
6v \\
0 \\
\end{pmatrix} , \quad \quad
\vec{v}_{\text{B}}(t) =
\begin{pmatrix}
0 \\
8v \\
\end{pmatrix} \\
\\
\vec{v}_{\text{A}}(t') &=&
\begin{pmatrix}
2v \\
5v \\
\end{pmatrix} , \quad \quad
\vec{v}_{\text{B}}(t') =
\begin{pmatrix}
v'_{\text{B}_x} \\
v'_{\text{B}_y} \\
\end{pmatrix}
\end{eqnarray*}
となる。
従って、運動量保存則は
\begin{eqnarray*}
m_{\text{A}} \vec{v}_{\text{A}} +m_{\text{B}} \vec{v}_{\text{B}} &=& m_{\text{A}} \vec{v}'_{\text{A}} +m_{\text{B}} \vec{v}'_{\text{B}} \\
\\
m_{\text{A}}
\begin{pmatrix}
6v \\
0 \\
\end{pmatrix}
+m_{\text{B}}
\begin{pmatrix}
0 \\
8v \\
\end{pmatrix} &=&
m_{\text{A}}
\begin{pmatrix}
2v \\
5v \\
\end{pmatrix}
+m_{\text{B}}
\begin{pmatrix}
v'_{\text{B}_x} \\
v'_{\text{B}_y} \\
\end{pmatrix}
\end{eqnarray*}
となる。
ここで、$m_{\text{A}}=m_{\text{B}}=m$より
\begin{eqnarray*}
6mv &=& 2mv +m v'_{\text{B}_x} \\
\\
8mv &=& 5mv +m v'_{\text{B}_y} \\
\end{eqnarray*}
よって、
\begin{eqnarray*}
6v &=& 2v + v'_{\text{B}_x} \\
\\
8v &=& 5v + v'_{\text{B}_y} \\
\end{eqnarray*}
となり、
\begin{eqnarray*}
v'_{\text{B}_x} &=& 4v \\
\\
v'_{\text{B}_y} &=& 3v \\
\end{eqnarray*}
となる。
従って、物体$\text{B}$の衝突後の速度$\vec{v}'_{\text{B}}$は
\begin{eqnarray*}
\vec{v}'_{\text{B}}=
\begin{pmatrix}
4v \\
3v \\
\end{pmatrix}
\end{eqnarray*}
となる。
(2)
\begin{eqnarray*}
\vec{I_{\text{B}}}=\vec{F}_{\text{B}} \Delta t = \Delta(m\vec{v}_{\text{B}}) &=& m\vec{v}'_{\text{B}} - m\vec{v}_{\text{B}} \\
\\
&=& m
\begin{pmatrix}
4v \\
3v \\
\end{pmatrix} - m
\begin{pmatrix}
0 \\
8v \\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
4mv \\
-5mv \\
\end{pmatrix} \\
\end{eqnarray*}
となる。
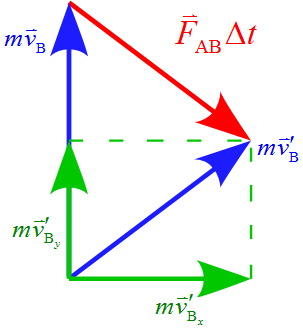
教科書的計算
(1) 運動量保存則より
\begin{eqnarray*}
6mv &=& 2mv +m v'_{\text{B}_x} \\
\\
8mv &=& 5mv +m v'_{\text{B}_y} \\
\end{eqnarray*}
より
\begin{eqnarray*}
v'_{\text{B}_x} &=& 4v \\
\\
v'_{\text{B}_y} &=& 3v \\
\end{eqnarray*}
となる。
(2) 物体$\text{B}$に加わった力積は、物体$\text{B}$の運動量の変化に等しいので
\begin{eqnarray*}
x \text{成分}&:& m\cdot 4v - m \cdot 0 = 4mv \\
\\
y \text{成分}&:& m\cdot 3v - m \cdot 8v = -5mv
\end{eqnarray*}
となる。