力のモーメント ~ 練習問題 part-3

力のモーメント ~ 練習問題 part-3

　力のモーメントに関連した練習問題を取り上げる。

壁に立てかけられた棒

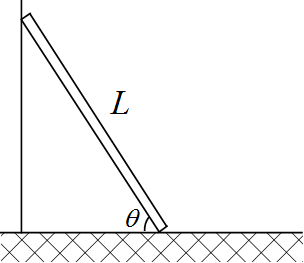
　図のような長さ$L$質量$m$の棒が鉛直の壁に立てかけられている。壁は滑らかであるが、床は洗い面であるとする。
　床と棒のなす角$\theta$を小さくすると棒は滑り出してしまう。滑り出す直前の角$\theta _0$の条件$\tan \theta _0$を求めよ。但し、静止摩擦係数は$\mu$として用いよ。

解答

位置ベクトル$\vec{r}_1 ,\ \vec{r}_2$を設定

　壁を原点$O$とし、下図の様に位置ベクトル$\vec{r}_1 ,\ \vec{r}_2$を設定する。

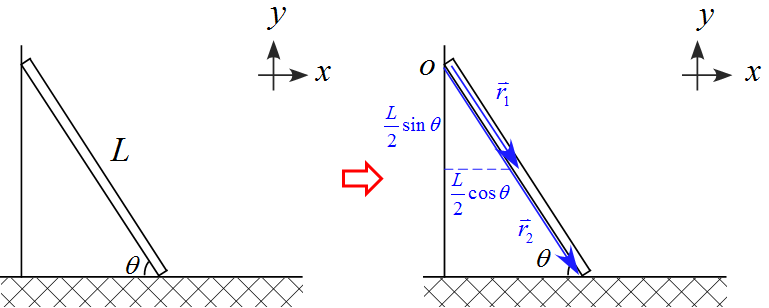
位置ベクトル$\vec{r}_1 ,\ \vec{r}_2$は
\begin{eqnarray*}
\vec{r}_1 &=&
\begin{pmatrix}
\frac{L}{2} \cos \theta \\
-\frac{L}{2} \sin \theta \\
0 \\
\end{pmatrix} ,\ \quad
\vec{r}_2 &=&
\begin{pmatrix}
L \cos \theta \\
-L \sin \theta \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}

である。

作用する力を書き込む

• 作用する力は棒の質量による重力$mg$、壁からの抗力$R'$、地面からの抗力$R$の3つである。
• 壁は摩擦力が無いので垂直抗力$N'(R')$とした。
• 地面からの抗力は垂直抗力$N$と摩擦力$f$に分解される。
• 重力$mg$は棒の重心に作用しているとする。

運動方程式を立てる

運動方程式は
\begin{eqnarray*}
m a_x &=&N' -f \\
\\
m a_y &=& N - mg
\end{eqnarray*}
と記述できる。
束縛条件より、$a_x =0, \ a_y =0$より
\begin{eqnarray*}
0 &=&N' -f \\
\\
0 &=& N - mg
\end{eqnarray*}
摩擦力$f=\mu N$と合わせると

\begin{eqnarray*}
N' &=& f = \mu mg \\
\\
N &=& mg
\end{eqnarray*}

となる。

作用する力をベクトルとして表す

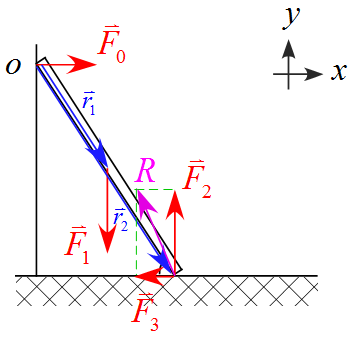
　作用する力をそれぞれ、$\vec{F}_0$から$\vec{F}_3$まで添え字を設定する。今回は壁を支点として計算するので$\vec{F}_0$は力のモーメントを生じないので、$\vec{F}_1$から$\vec{F}_3$を書き出すと

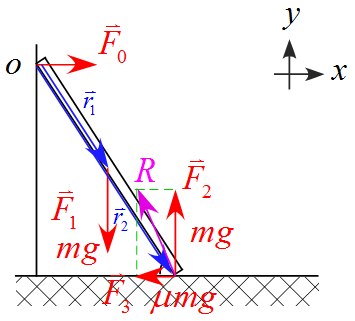
作用する力$\vec{F}_1 ,\ \vec{F}_2 ,\ \vec{F}_3$は
\begin{eqnarray*}
\vec{F}_1 &=&
\begin{pmatrix}
0 \\
-mg \\
0 \\
\end{pmatrix} ,\ \quad
\vec{F}_2 &=&
\begin{pmatrix}
0 \\
mg \\
0 \\
\end{pmatrix}
,\ \quad
\vec{F}_3 &=&
\begin{pmatrix}
-\mu mg \\
0 \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}

である。

力のモーメントを計算する

外積を使って計算

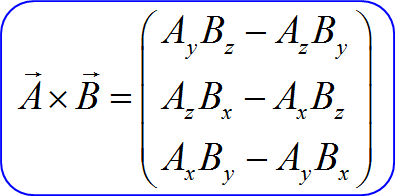
\begin{eqnarray*}
\vec{M}_1 = \vec{r}_1 \times \vec{F}_1 &=&
\begin{pmatrix}
\frac{L}{2} \cos \theta \\
-\frac{L}{2} \sin \theta \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
0 \\
-mg \\
0 \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
\frac{L}{2} \cos \theta \cdot (-mg) - \left(-\frac{L}{2} \sin \theta \right) \cdot 0 \\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
-\frac{L}{2}mg \cos \theta \\
\end{pmatrix}
\end{eqnarray*}

\begin{eqnarray*}
\vec{M}_2 = \vec{r}_2 \times \vec{F}_2 &=&
\begin{pmatrix}
L \cos \theta \\
-L \sin \theta \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
0 \\
mg \\
0 \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
L \cos \theta \cdot mg - \left(-L \sin \theta \right) \cdot 0 \\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
L mg \cos \theta \\
\end{pmatrix}
\end{eqnarray*}

\begin{eqnarray*}
\vec{M}_3 = \vec{r}_2 \times \vec{F}_3 &=&
\begin{pmatrix}
L \cos \theta \\
-L \sin \theta \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
-\mu mg \\
0 \\
0 \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
L \cos \theta \cdot 0 - \left(-L \sin \theta \right) \cdot (-\mu mg) \\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
-L \mu mg \sin \theta \\
\end{pmatrix}
\end{eqnarray*}

• 位置ベクトル$\vec{r}$も作用する力$\vec{F}$も$z$成分を持たないため、外積の結果の$x,y$成分は外積の性質より計算せずに$0$と記述した。

従って、力のモーメント$\vec{M}$は

\begin{eqnarray*}
\vec{M} &=& \vec{M}_1 + \vec{M}_2 + \vec{M}_3 \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
-\frac{L}{2}mg \cos \theta \\
\end{pmatrix} +
\begin{pmatrix}
0 \\
0 \\
L mg \cos \theta \\
\end{pmatrix} +
\begin{pmatrix}
0 \\
0 \\
-L \mu mg \sin \theta \\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
-\frac{L}{2}mg \cos \theta + L mg \cos \theta- L \mu mg \sin \theta \\
\end{pmatrix}
\end{eqnarray*}

となる。

回転しない条件

回転の運動方程式において、回転しない条件は$\theta = \theta_0$のとき

\begin{eqnarray*}
\frac{\diff \vec{L}}{\diff t} &=& \vec{M} =\vec{0} \\
\\
\begin{pmatrix}
\frac{\diff \vec{L}_x}{\diff t} \\
\frac{\diff \vec{L}_y}{\diff t} \\
\frac{\diff \vec{L}_z}{\diff t} \\
\end{pmatrix} &=&
\begin{pmatrix}
0 \\
0 \\
-\frac{L}{2}mg \cos \theta_0 + L mg \cos \theta_0 - L \mu mg \sin \theta_0 \\
\end{pmatrix} =
\begin{pmatrix}
0 \\
0 \\
0 \\
\end{pmatrix}
\end{eqnarray*}
であるから、$z$成分が$0$になればよい。
即ち、

\begin{eqnarray*}
\frac{\diff \vec{L}_z}{\diff t} = -\frac{L}{2}mg \cos \theta_0 + L mg \cos \theta_0 - L \mu mg \sin \theta_0 =0
\end{eqnarray*}

である。
式を整理するために$mgL \cos \theta_0$で両辺を割ると

\begin{eqnarray*}
\frac{ -\frac{L}{2}mg \cos \theta_0}{mgL \cos \theta_0} + \frac{L mg \cos \theta_0}{mgL \cos \theta_0} - \frac{ L \mu mg \sin \theta_0}{mgL \cos \theta_0} &= & 0 \\
\\
-\frac{1}{2} + 1 - \frac{\mu \sin \theta_0}{\cos \theta_0} &=&0 \\
\\
\mu \tan \theta_0 &=& \frac{1}{2} \\
\\
\tan \theta_0 &=& \frac{1}{2 \mu}
\end{eqnarray*}

となる。