等速度運動 (等速直線運動)

等速度運動 (等速直線運動)

　前回の練習問題では「速度が一定である～」と言った表現で何も説明していないが、「速度が一定」な運動は「等速度運動」と名前がついている。文字通り、「速度が等しい」運動を指している。速度は大きさと向きを持ったベクトル量である。つまり、速度が等しいという事は、「速さ」も等しく「向きも変化しない直線運動」である事になるので、「等速度運動」を別名で「等速直線運動」と呼ぶこともある。
　今回はこの「等速度運動」について解説していく。

　等速度運動は速度の定義$v=\displaystyle \frac{\diff x}{\diff t}$より、

\begin{eqnarray*}
v=\frac{\diff x}{\diff t} = v_0 \ \ \text{(一定)}
\end{eqnarray*}

と表される。

$v-t$グラフ

　$v-t$グラフは

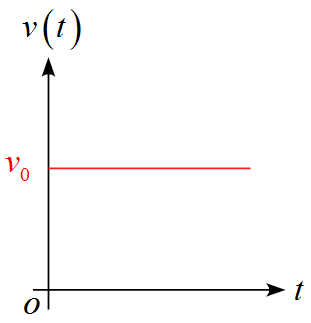
となる。

• 速度$v$は常に$v_0$で一定である。
• $v(t)=v_0$と表される

$x-t$グラフ

　$v-t$グラフは

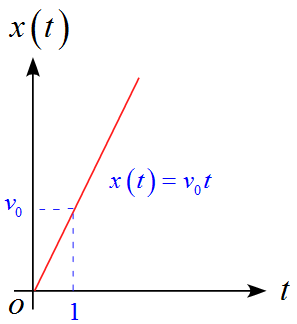
となる。

• 速度の定義より、速度は$x-t$グラフの傾きを表している。
• 傾きは一定値$v_0$である。
• $x(t)=v_0 t$と表される

変位について

　速度の定義より$v=\displaystyle \frac{\diff x}{\diff t}$

\begin{eqnarray*}
\bar{v} &=& \frac{\Delta x}{\Delta t} \\
\\
\Delta x &=& \bar{v} \cdot \Delta t \\
\\
&=& v_0 \cdot \Delta t \\
\end{eqnarray*}

となる。

　ここで、$x(0)=0, \ x(t)=x$とすると

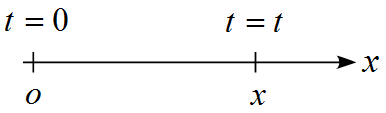
\begin{eqnarray*}
\Delta x &=& v_0 \cdot \Delta t \\
\\
x-0 &=& v_0 \cdot (t-0)\\
\\
x &=& v_0 \cdot t
\end{eqnarray*}

となる。

　初期位置が$x(0)=x_0$の場合、

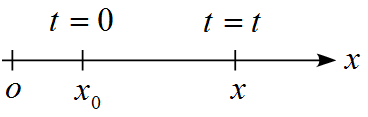
\begin{eqnarray*}
\Delta x &=& v_0 \cdot \Delta t \\
\\
x-x_0 &=& v_0 \cdot (t-0)\\
\\
x &=& v_0 \cdot t + x_0
\end{eqnarray*}

となる。

$v=\frac{\diff x}{\diff t}$を$t$で積分する

　高校物理の範囲からは超えるが、数学の内容自体は高校数学の範囲である。

　速度$v_0=\text{一定}$として計算すると

\begin{eqnarray*}
\frac{\diff x}{\diff t} &=& v_0 \\
\\
\int \frac{\diff x}{\diff t} \diff t &=& \int v_0 \diff t \\
\\
\int \diff x &=& \int v_0 \diff t \\
\\
x &=& v_0 t+C \ \ \text{(C:積分定数)}
\end{eqnarray*}

となる。ここで、初期条件$x(0)=x_0$とすると

\begin{eqnarray*}
x(0) = v_0 \cdot 0+C &=& x_0 \\
\\
C &=& x_0
\end{eqnarray*}
となり、

\begin{eqnarray*}
x(t) = v_0 t +x_0
\end{eqnarray*}
となる。

　速度$v=\displaystyle \frac{\diff x}{\diff t}$を積分するという事は、$v-t$グラフの面積を求めることに等しい。即ち、「変位の大きさは$v-t$グラフの面積」であることが数学的にも確認できる。