速度はベクトル ~ 速度の合成・分解

速度はベクトル ~ 速度の合成・分解

　既に何度も登場している通り「速度はベクトル量」である。つまり、速度の合成や分解がベクトルとして計算できることになる。

速度ベクトルの合成

　船が川を横切るような運動をする場合を例に取ると、川の流れの速度を$\vec{v}_1$とし、船の川の水に対する速度を$\vec{v}_2$とする。すると、岸辺からこの船を見た場合、川の流れの速度$\vec{v}_1$と船の速度$\vec{v}_2$を合成した速度として観測されることになる。

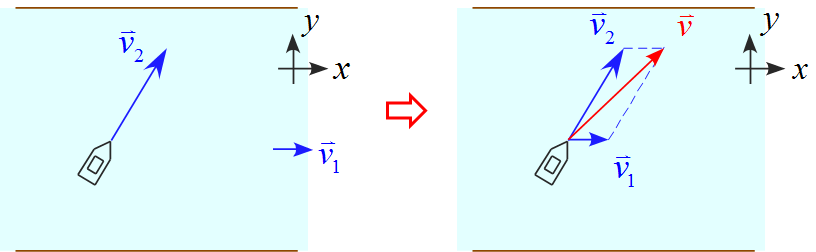
　この合成された速度を「合成速度」と呼び、

\begin{eqnarray*}
\vec{v} = \vec{v}_1 + \vec{v}_2
\end{eqnarray*}

となる。

速度ベクトルの分解

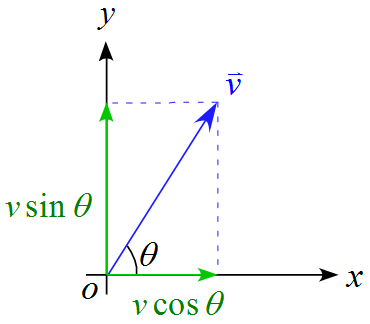
　速度$\vec{v}$を$x,y$軸に沿って成分を分解するとすると、下図のようになり、

\begin{eqnarray*}
v_x &=& v \cos \theta \\
\\
v_y &=& v \sin \theta
\\\\
|\vec{v}| &=& \sqrt{v_x^2 +v_y^2}
\end{eqnarray*}
となる。

　分解された速度$\vec{v}_x, \ \vec{v}_y$を「分速度」と呼ぶ

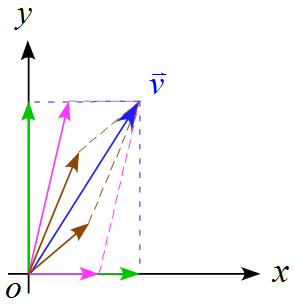
　平行四辺形さえ作れればベクトルの分解はできる。
従って、下図のようにベクトルの分解は無数に存在するので意味のある分解を用いることになる。