仕事~ 練習問題 part-2
仕事に関連した練習問題を取り上げる。今回は斜面を扱ったモデルを解説する。
滑らかな斜面上の物体に水平に力を加える
なめらかな斜面上に置いた物体に水平方向に一定の大きさの力$F$を加え続けたところ斜面に沿って上向に$L$だけ移動した。この運動での加えた力$F$がした仕事を求めよ。
但し、水平面と斜面のなす角を$\theta$とする。
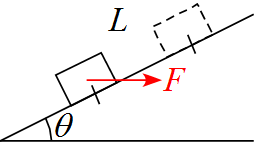
解答
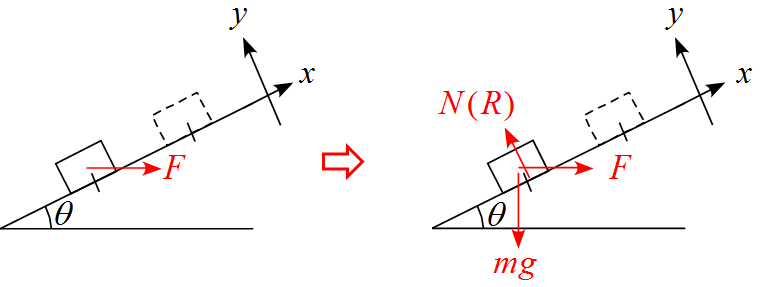
軸を設定し、作用する力を書き込む
- 斜面に沿って上向きを$x$軸の正に、斜面に垂直な方向上向きを$y$軸の正に設定する。
- 作用する力は重力$mg\ $面からの抗力$N(R), \ $作用させる力$F$の3つである。
斜面に沿った成分に分解すると
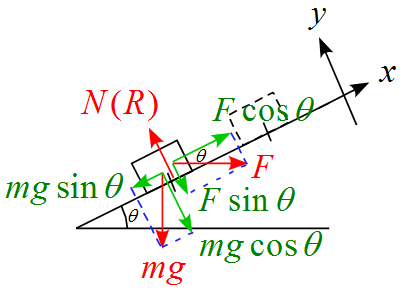
となる。
運動方程式を立てる。
運動方程式は
\begin{eqnarray*}
ma_x &=& - mg \sin \theta + F \cos \theta \\
\\
ma_y &=& N - mg \cos \theta - F \sin \theta
\end{eqnarray*}
となる。
束縛条件 $a_y =0$ より
\begin{eqnarray*}
ma_x &=& - mg \sin \theta + F \cos \theta \\
\\
0 &=& N - mg \cos \theta - F \sin \theta
\end{eqnarray*}
となる。
$x$方向の運動方程式に対して$x$で積分すると
\begin{eqnarray*}
ma_x &=& - mg \sin \theta + F \cos \theta \\
\\
\int m \frac{\diff v_x}{\diff t} \diff x &=& \int (- mg \sin \theta + F \cos \theta ) \diff x \\
\\
\int m \frac{\diff v_x}{\diff t} v_x \diff t &=& \int (- mg \sin \theta + F \cos \theta ) \diff x \\
\\
\int \frac{\diff }{\diff t} \left( \frac{1}{2}mv_x^2 \right) \diff t&=& \int (- mg \sin \theta ) \diff x + \int F \cos \theta \diff x \\
\\
\end{eqnarray*}
となる。

従って、加えた力$F$がした仕事$W_F$は移動した距離が$L$なので
\begin{eqnarray*}
W_F &=& \int F \cos \theta \diff x \\
\\
&=& \int_0^L F \cos \theta \diff x \\
\\
&=& \left[ (F \cos \theta) x \right]_0^L \\
\\
&=& (F \cos \theta)\cdot L - (F \cos \theta) \cdot 0 \\
\\
&=& F L \cos \theta
\end{eqnarray*}
となる。
- 運動方程式を立てればどの仕事に対応するか正負を含めて理解しやすい。従って、単に仕事を求めるだけで運動方程式を直接使用しない問題でも運動方程式を立てるべきである。
教科書的計算
加えた力を軸に沿って成分を分解すると下図のようになる。
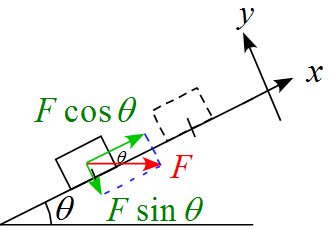
加えた力$F$がした仕事$W_F$は移動した距離が$L$なので
\begin{eqnarray*}
W_F &=& \text{力} \times \text{移動した距離} \\
\\
&=& F \cos \theta \cdot L \\
\\
&=& FL \cos \theta
\end{eqnarray*}
となる。