運動量と力積~ 練習問題 part-3
今回は運動量と力積に関連した基礎的な練習問題を取り上げる。
斜衝突 ~ 静止している物体に衝突する
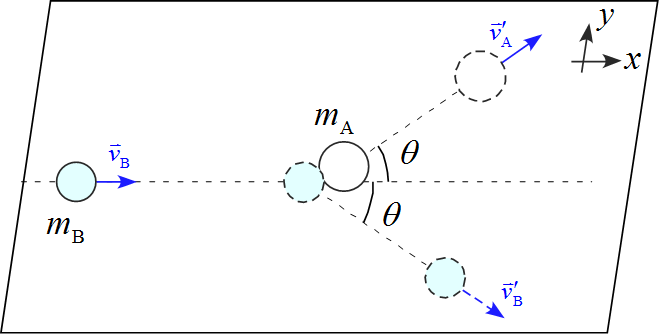
なめらかな水平面上で静止していた質量$m_{\text{A}}$の物体$\text{A}$に、速度$\vec{v}_{\text{B}}$で進んできた質量$m_{\text{B}}$の物体$\text{B}$が衝突した。衝突後、物体$\text{A}, \ \text{B}$はそれぞれ図の方向に進んだ。それぞれの質量は$m_{\text{A}}=2m_{\text{B}}=2m$として、衝突後の物体$\text{A}, \ \text{B}$の速度$\vec{v}'_{\text{A}} , \vec{v}'_{\text{B}}$をそれぞれ求めよ。
解答
軸を設定し、作用する力を書き込む
- $x$軸の正の向きは右側に、$y$軸の正の向きは上に設定した。
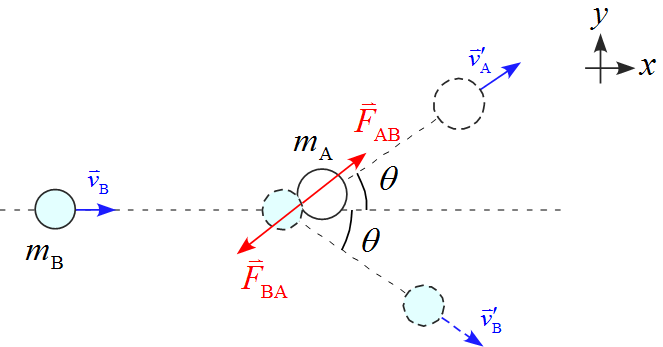
- 2物体が衝突する瞬間に受ける力は物体$\text{A}$が物体$\text{B}$から受ける力$\vec{F}_{\text{AB}}$と物体$\text{B}$が物体$\text{A}$から受ける力$\vec{F}_{\text{BA}}$の2つである。
- 作用する力に重力$mg$となめらかな水平面から受ける効力$R(N)$があるが、$z$軸上での作用となるので省略した。
運動方程式を立てる
運動方程式は物体$\text{A}$について
\begin{eqnarray*}
m_{\text{A}} a_{\text{A}} &=& \vec{F}_{\text{AB}} \\
\\
m_{\text{A}} \frac{\diff \vec{v}_{\text{A}}}{\diff t} &=& \vec{F}_{\text{AB}} \\
\\
\frac{\diff}{\diff t} (m_{\text{A}} \vec{v}_{\text{A}}) &=& \vec{F}_{\text{AB}}
\end{eqnarray*}
となる。
運動方程式は物体$\text{B}$について
\begin{eqnarray*}
m_{\text{B}} a_{\text{B}} &=& \vec{F}_{\text{BA}} \\
\\
m_{\text{B}} \frac{\diff \vec{v}_{\text{B}}}{\diff t} &=& \vec{F}_{\text{BA}} \\
\\
\frac{\diff}{\diff t} (m_{\text{B}} \vec{v}_{\text{B}}) &=& \vec{F}_{\text{BA}}
\end{eqnarray*}
となる。
ここで、$\vec{F}_{\text{AB}}$と$\vec{F}_{\text{BA}}$は作用反作用の関係であるので、この力の大きさを$F$とおくと
\begin{eqnarray*}
\vec{F}_{\text{AB}} &=& \vec{F}
\\
\vec{F}_{\text{BA}} &=& -\vec{F}
\end{eqnarray*}
となるので
\begin{eqnarray*}
\frac{\diff}{\diff t} (m_{\text{A}} \vec{v}_{\text{A}}) &=& \vec{F}
\\
\frac{\diff}{\diff t} (m_{\text{B}} \vec{v}_{\text{B}}) &=& -\vec{F}
\end{eqnarray*}
となる。
2式の和をとると
\begin{eqnarray*}
\frac{\diff}{\diff t} (m_{\text{A}} \vec{v}_{\text{A}}) + \frac{\diff}{\diff t} (m_{\text{B}} \vec{v}_{\text{B}}) &=& \vec{F} +(-\vec{F}) \\
\\
\frac{\diff}{\diff t} (m_{\text{A}} \vec{v}_{\text{A}} +m_{\text{B}} \vec{v}_{\text{B}} ) &=& \vec{0}
\end{eqnarray*}
となり、物体$\text{AB}$の衝突において運動量は保存していると言える。

従って、
\begin{eqnarray*}
m_{\text{A}} \vec{v}_{\text{A}} +m_{\text{B}} \vec{v}_{\text{B}} = m_{\text{A}} \vec{v}'_{\text{A}} +m_{\text{B}} \vec{v}'_{\text{B}}
\end{eqnarray*}
の関係式が導き出される。

運動量保存則を適用する
前述の通り、運動量保存則が成立することが確認できなので、これを適用していく。
問題の条件は
\begin{eqnarray*}
\vec{v}_{\text{A}}(t) &=&
\begin{pmatrix}
0 \\
0 \\
\end{pmatrix} , \quad \quad
\vec{v}_{\text{B}}(t) =
\begin{pmatrix}
v_{\text{B}} \\
0 \\
\end{pmatrix} \\
\\
\vec{v}_{\text{A}}(t') &=&
\begin{pmatrix}
v'_{\text{A}} \cos \theta \\
v'_{\text{A}} \sin \theta \\
\end{pmatrix} , \quad \quad
\vec{v}_{\text{B}}(t') =
\begin{pmatrix}
v'_{\text{B}} \cos \theta \\
-v'_{\text{B}} \sin \theta \\
\end{pmatrix}
\end{eqnarray*}
となる。
従って、運動量保存則は
\begin{eqnarray*}
m_{\text{A}} \vec{v}_{\text{A}} +m_{\text{B}} \vec{v}_{\text{B}} &=& m_{\text{A}} \vec{v}'_{\text{A}} +m_{\text{B}} \vec{v}'_{\text{B}} \\
\\
m_{\text{A}}
\begin{pmatrix}
0 \\
0 \\
\end{pmatrix}
+m_{\text{B}}
\begin{pmatrix}
v_{\text{B}} \\
0 \\
\end{pmatrix} &=&
m_{\text{A}}
\begin{pmatrix}
v'_{\text{A}} \cos \theta \\
v'_{\text{A}} \sin \theta \\
\end{pmatrix}
+m_{\text{B}}
\begin{pmatrix}
v'_{\text{B}} \cos \theta \\
-v'_{\text{B}} \sin \theta \\
\end{pmatrix}
\end{eqnarray*}
となる。
よって、
\begin{eqnarray*}
m_{\text{B}} v_{\text{B}} &=& m_{\text{A}} v'_{\text{A}} \cos \theta + m_{\text{B}} v'_{\text{B}} \cos \theta \\
\\
0 &=& m_{\text{A}} v'_{\text{A}} \sin \theta - m_{\text{B}} v'_{\text{B}} \sin \theta \\
\end{eqnarray*}
となる。
ここで、$m_{\text{A}}=2m_{\text{B}}=2m$より
\begin{eqnarray*}
m v_{\text{B}} &=& 2m v'_{\text{A}} \cos \theta + m v'_{\text{B}} \cos \theta \\
\\
0 &=& 2m v'_{\text{A}} \sin \theta - m v'_{\text{B}} \sin \theta \\
\end{eqnarray*}
両辺$m$で割ると
\begin{eqnarray*}
v_{\text{B}} &=& 2 v'_{\text{A}} \cos \theta + v'_{\text{B}} \cos \theta \\
\\
0 &=& 2 v'_{\text{A}} \sin \theta - v'_{\text{B}} \sin \theta \\
\end{eqnarray*}
それぞれの式に$\sin \theta ,\ \cos \theta$をかけて和を取ると
\begin{eqnarray*}
v_{\text{B}} \sin \theta &=& 2 v'_{\text{A}} \cos \theta \sin \theta + v'_{\text{B}} \cos \theta \sin \theta \\
\\
0 &=& 2 v'_{\text{A}} \sin \theta \cos \theta - v'_{\text{B}} \sin \theta \cos \theta \\
\\
\hline
\\
v_{\text{B}} \sin \theta &=& 4 v'_{\text{A}} \sin \theta \cos \theta \\
\\
v_{\text{B}} &=& 4 v'_{\text{A}} \cos \theta \\
\\
v'_{\text{A}} &=& \frac{v_{\text{B}}}{4 \cos \theta}
\end{eqnarray*}
また、$v'_{\text{B}}$は
\begin{eqnarray*}
v'_{\text{B}} \sin \theta &=& 2 v'_{\text{A}} \sin \theta \\
\\
v'_{\text{B}} &=& 2 v'_{\text{A}} \\
\\
&=& \frac{v_{\text{B}}}{2 \cos \theta}
\end{eqnarray*}
となる。
従って
\begin{eqnarray*}
\vec{v}'_{\text{A}} &=& \vec{v}_{\text{A}}(t') &=&
\begin{pmatrix}
v'_{\text{A}} \cos \theta \\
v'_{\text{A}} \sin \theta \\
\end{pmatrix} =
\begin{pmatrix}
\frac{v_{\text{B}}}{4 \cos \theta} \cos \theta \\
\frac{v_{\text{B}}}{4 \cos \theta} \sin \theta \\
\end{pmatrix} =
\begin{pmatrix}
\frac{1}{4} v_{\text{B}} \\
\frac{1}{4} v_{\text{B}} \tan \theta \\
\end{pmatrix}
\\ \\
\vec{v}'_{\text{B}} &=& \vec{v}_{\text{B}}(t') &=&
\begin{pmatrix}
v'_{\text{B}} \cos \theta \\
-v'_{\text{B}} \sin \theta \\
\end{pmatrix} =
\begin{pmatrix}
\frac{v_{\text{B}}}{2 \cos \theta} \cos \theta \\
-\frac{v_{\text{B}}}{2 \cos \theta} \sin \theta \\
\end{pmatrix} =
\begin{pmatrix}
\frac{1}{2} v_{\text{B}} \\
-\frac{1}{2} v_{\text{B}} \tan \theta \\
\end{pmatrix}
\end{eqnarray*}
となる。
教科書的計算
教科書では運動量保存則の成立は特に確認しないでも利用しているようである。よって、いきなり「運動量保存則より」と記述していく。
運動量保存則より、
\begin{eqnarray*}
m_{\text{B}} v_{\text{B}} &=& m_{\text{A}} v'_{\text{A}} \cos \theta + m_{\text{B}} v'_{\text{B}} \cos \theta \\
\\
0 &=& m_{\text{A}} v'_{\text{A}} \sin \theta - m_{\text{B}} v'_{\text{B}} \sin \theta \\
\end{eqnarray*}
となる。
ここで、$m_{\text{A}}=2m_{\text{B}}=2m$より
\begin{eqnarray*}
m v_{\text{B}} &=& 2m v'_{\text{A}} \cos \theta + m v'_{\text{B}} \cos \theta \\
\\
0 &=& 2m v'_{\text{A}} \sin \theta - m v'_{\text{B}} \sin \theta \\
\end{eqnarray*}
となる。
式を整理して(詳細は前述の通り)
\begin{eqnarray*}
v'_{\text{A}} &=& \frac{v_{\text{B}}}{4 \cos \theta} \\
\\
v'_{\text{B}} &=& \frac{v_{\text{B}}}{2 \cos \theta}
\end{eqnarray*}
となる。