運動量と力積~ 練習問題 part-4
今回は運動量と力積に関連した基礎的な練習問題を取り上げる。
質量が変化する運動
質量$M,\ $速度$V$で宇宙空間を飛んでいるロケットが、質量$m$の燃焼ガスを後方に噴出した。噴出された燃焼ガスはロケットと逆向きに速度$-v$で飛んでいったとする。噴出後のロケットの速度を求めよ。
但し、燃焼ガスの噴出は瞬間的であるとする。
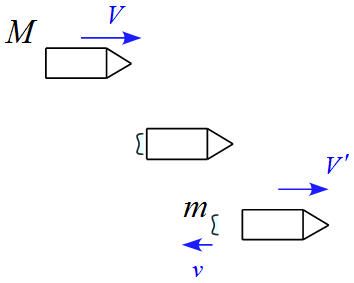
解答
軸を設定し、作用する力を書き込む
- $x$軸の正の向きは右側に設定した。
- 噴出する瞬間に受ける力はロケット(rocket)が燃料ガス(fuel)から受ける力$\vec{F}_{\text{RF}}$と燃料ガスがロケットから受ける力$\vec{F}_{\text{FR}}$の2つである。
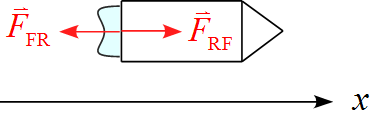
運動方程式を立てる
運動方程式は質量が変化する運動なので、ニュートンが最初に提唱した形で適用する。
ロケットについて
\begin{eqnarray*}
\frac{\diff}{\diff t} [(M-m) \vec{v}_{\text{R}}] = \vec{F}_{\text{RF}}
\end{eqnarray*}
となる。
燃焼ガスについて
\begin{eqnarray*}
\frac{\diff}{\diff t}(m \vec{v}_{\text{F}}) = \vec{F}_{\text{FR}}
\end{eqnarray*}
となる。
ここで、$\vec{F}_{\text{RF}}$と$\vec{F}_{\text{FR}}$は作用反作用の関係であるので、この力の大きさを$F$とおくと
\begin{eqnarray*}
\frac{\diff}{\diff t} [(M-m) \vec{v}_{\text{R}}] &=& \vec{F}_{\text{RF}} = \vec{F}\\
\\
\frac{\diff}{\diff t}(m \vec{v}_{\text{F}}) &=& \vec{F}_{\text{FR}} = -\vec{F} \\
\\
\hline
\\
\frac{\diff}{\diff t} [(M-m) \vec{v}_{\text{R}} + m \vec{v}_{\text{F}} ] &=& 0
\end{eqnarray*}
となるので運動量は保存していると言える。

運動量保存則を適用する
前述の通り、運動量保存則が成立することが確認できなので、これを適用していく。
問題の条件は
\begin{eqnarray*}
\vec{v}_{\text{R}}(t) &=&
\begin{pmatrix}
V \\
0 \\
\end{pmatrix} , \quad \quad
\vec{v}_{\text{F}}(t) =
\begin{pmatrix}
V \\
0 \\
\end{pmatrix} \quad \quad (一体となって運動) \\
\\
\vec{v}_{\text{R}}(t') &=&
\begin{pmatrix}
V' \\
0 \\
\end{pmatrix} , \quad \quad
\vec{v}_{\text{F}}(t') =
\begin{pmatrix}
-v \\
0 \\
\end{pmatrix}
\end{eqnarray*}
となる。
従って、運動量保存則は
\begin{eqnarray*}
(M-m) \vec{v}_{\text{R}} +m \vec{v}_{\text{F}} &=& (M-m) \vec{v}'_{\text{R}} +m \vec{v}'_{\text{F}} \\
\\
(M-m)
\begin{pmatrix}
V \\
0 \\
\end{pmatrix}
+m
\begin{pmatrix}
V \\
0 \\
\end{pmatrix} &=&
(M-m)
\begin{pmatrix}
V' \\
0 \\
\end{pmatrix}
+m
\begin{pmatrix}
-v \\
0 \\
\end{pmatrix}
\end{eqnarray*}
となる。
よって、
\begin{eqnarray*}
(M-m)V +mV &=& (M-m)V' -mv \\
\\
MV+mv &=& (M-m)V' \\
\\
V' &=& \frac{MV+mv}{M-m}
\end{eqnarray*}
となる。
教科書的計算
運動量保存則より、
\begin{eqnarray*}
(M-m)V +mV &=& (M-m)V' -mv \\
\end{eqnarray*}
と記述し、
式を整理し
\begin{eqnarray*}
V' &=& \frac{MV+mv}{M-m}
\end{eqnarray*}
となる。