加速度(acceleration)の定義
車を運転しているとき、アクセルを踏み込んで「加速」したり、ブレーキを踏んで「減速」したりする。普段の生活の中で何気なく使っている「加速」という言葉を物理ではどのような意味を持つのか考える。
ここでは、加速度の定義について解説していく。
加速度の定義
物体がある時刻$t$で点$\text{P}$の位置で速度$\vec{v}$であり、時刻$t + \Delta t $で点$\text{P}$で速度$\vec{v}'$であったとする。つまり、時間$\Delta t$の間に速度が$\Delta \vec{v}$変化したとする。

単位時間あたりの速度変化(時間に対する速度変化率)は
\begin{eqnarray*}
\frac{\Delta \vec{v}}{\Delta t} &=& \frac{\vec{v}' - \vec{v}}{\Delta t} = \frac{\vec{v}(t+\Delta t) - \vec{v}(t)}{\Delta t} = \text{平均の加速度}
\end{eqnarray*}
ここで$\Delta t =0$の極限を考えると
\begin{eqnarray*}
\lim_{\Delta t \to 0} \frac{\Delta \vec{v}}{\Delta t} = \lim_{\Delta t \to 0} \frac{\vec{v}(t+\Delta t) - \vec{v}(t)}{\Delta t} = \frac{\diff \vec{v}}{\diff t}
\end{eqnarray*}
これを速度$\vec{a}$と定義する。
$\vec{r}$の2階微分
速度の定義$\displaystyle \vec{v}=\frac{\diff \vec{x}}{\diff t} $より加速度$\vec{a}$は
\begin{eqnarray*}
\vec{a} &=& \frac{\diff \vec{v}}{\diff t} = \frac{\diff }{\diff t} \left( \vec{v} \right) \\
\\
&=& \frac{\diff }{\diff t} \left( \frac{\diff \vec{x} }{\diff t} \right) \\
\\
&=& \frac{\diff ^2 \vec{r} }{\diff t^2}
\end{eqnarray*}
と表すことができる。
加速度(acceleration)のまとめ
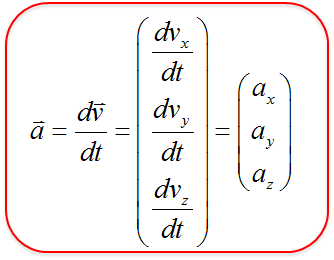
加速度の場合も$x,\ y, \ z$成分ごとに独立して考えることができる。