変位と距離

変位と距離

• 変位はベクトル量(大きさと向きを持つ)である。
• 距離はスカラー量(大きさのみ)である。
• 移動距離を考えた場合、変位の大きさと一致しない場合もある。

直線運動

　$x$軸上を運動する物体が$t=t_1$で$x_1$の位置にあり、$t=t_2$に$x_2$にあったとする。この時の変位$\Delta \vec{x}$は下図のように表される。

　変位$\Delta \vec{x}$の大きさ$|\Delta \vec{x}|$は
\begin{eqnarray*}
|\Delta \vec{x}| = x_2 -x_2
\end{eqnarray*}
となる。

　一方、同様の設定で、$t=t_1$で$x_1$の位置にあり、$t=t_2$に$x_2$を通過して$x_3$をまで行った後、$t=t_3$で$x_2$まで戻ってきたとする。

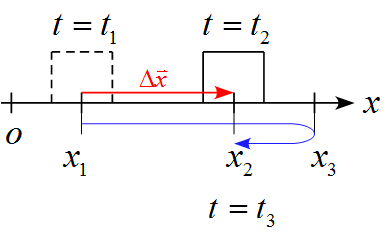
　この時、物体が移動した距離は$x$軸方向に進んだ距離$x_3 - x_1$と戻ってきた分の距離$x_3 - x_2$の合計となり、変位$\Delta \vec{x}$の大きさとは異なった値になることに注意したい。

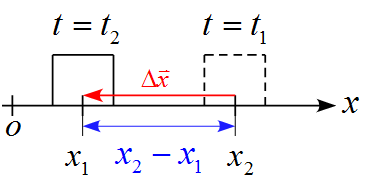
　また、下図のように、$t=t_1$で$x_2$の位置にあり、$t=t_2$に$x_1$に移動した場合では変位がマイナス方向となり、移動距離と変位$\Delta \vec{x}$の大きさは等しいが運動は逆方向となることも注意するべきである。

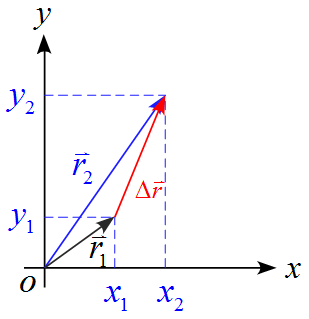
平面内の運動

　変位$\Delta \vec{r}$は

\begin{eqnarray*}
\Delta \vec{r} &=& \vec{r}_2 - \vec{r}_1 \\
\\
&=&
\begin{pmatrix}
x_2 \\
y_2 \\
\end{pmatrix} -
\begin{pmatrix}
x_1 \\
y_1 \\
\end{pmatrix}
\end{eqnarray*}

となる。$x, y$軸で分けて表すと

\begin{eqnarray*}
\Delta \vec{x} &=& x_2 -x_1\\
\\
\Delta \vec{y} &=& y_2 -y_1\\
\end{eqnarray*}
となる。

　従って、変位$\Delta \vec{r}$の大きさ$|\Delta \vec{r}|$は

\begin{eqnarray*}
|\Delta \vec{r}| =\sqrt{ (x_2 -x_1)^2 +(y_2 - y_1)^2 }
\end{eqnarray*}
となる。