エネルギー
「仕事とエネルギーの関係」の記事で解説した式は
\begin{eqnarray*}
\int \frac{\diff }{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t = \int \vec{F} \cdot \diff \vec{r}
\end{eqnarray*}
である。
ここ数回の解説では右辺の「仕事」を中心に取り扱ってきたが、ここからは左辺も含めて解説していく。
エネルギーとは何か?
一般用語として「エネルギー」という言葉は広く使われているが、物理学では「エネルギー」を「仕事をする能力」と考える。「仕事とエネルギーの関係式」を見てもわかるように、「仕事」と「エネルギー」は同じ次元の物理量として扱う。
かなり乱暴に言うと、運動方程式を$m\vec{a}=\vec{F}$と記述し、この両辺を$\vec{r}$の内積を取って積分して導かれた式の右辺の項を「仕事」と呼び、左辺にある項を「エネルギー」と呼ぶ。従って、左辺にある項を右辺に移項すると「エネルギー」と呼び名が変わることとなる。
具体例を扱いながら解説していく。
自由落下とエネルギー
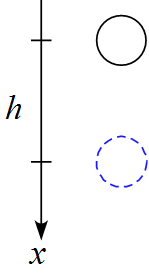
軸を設定し、作用する力を書き込む
- 下向きを$x$軸の正に設定する。
- 作用する力は重力$mg\ $のみである。
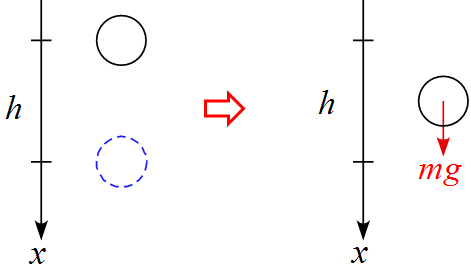
運動方程式を立てる
運動方程式は
\begin{eqnarray*}
ma &=& mg \\
\\
m\frac{\diff v}{\diff t} &=& mg
\end{eqnarray*}
となる。
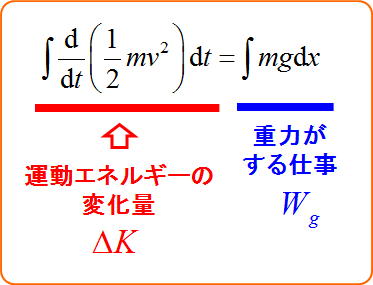
仕事を計算する ~ 両辺を$x$で積分する
\begin{eqnarray*}
m\frac{\diff v}{\diff t} &=& mg \\
\\
\int m\frac{\diff v}{\diff t} \diff x&=& \int mg \diff x\\
\\
\int m\frac{\diff v}{\diff t} v \diff t&=& \int mg \diff x \\
\\
\int \frac{\diff }{\diff t} \left( \frac{1}{2} m v^2 \right) \diff t&=& \int mg \diff x \\
\\
\end{eqnarray*}
となる。
初期条件を$v(0)=v_0=0 ,\ v(t)=v ,\ x(0) =x_0 ,\ x(t) =x $とすると、
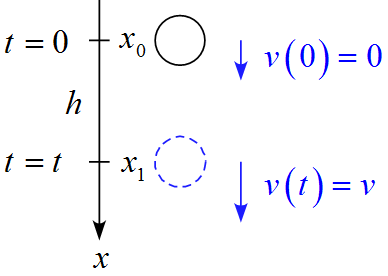
\begin{eqnarray*}
\int_0^t \frac{\diff }{\diff t} \left( \frac{1}{2} m v^2 \right) \diff t&=& \int_{x_0}^{x} mg \diff x \\
\\
\left[ \frac{1}{2} m v^2(t) \right] _{0}^{t} &=& [mgx]_{x_0}^{x} \\
\\
\frac{1}{2} mv^2 (t) - \frac{1}{2} mv^2 (0) &=& mgx - mg x_0 \\
\\
\frac{1}{2} mv^2- \frac{1}{2} m \cdot 0^2 &=& mg (x - x_0) \\
\\
\frac{1}{2} mv^2 &=& mgh
\end{eqnarray*}
となる。

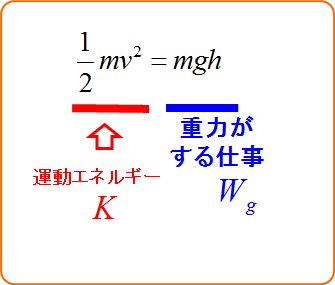
さらに、左辺に移項すると
\begin{eqnarray*}
\frac{1}{2} mv^2 +( -mgh) = 0
\end{eqnarray*}
となる。
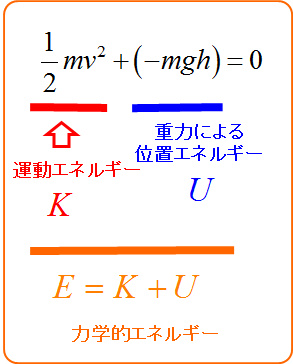
この式がエネルギー保存則を示している。保存則については別途解説する。
教科書的計算
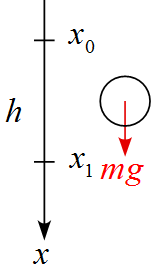
運動方程式は
\begin{eqnarray*}
ma = mg
\end{eqnarray*}
となる。
従って、この運動は$a=g = \text{const.}$の等加速度運動である。
等加速度運動の速度と距離の関係式の両辺に$\displaystyle \frac{1}{2}m$をかけると
\begin{eqnarray*}
v^2 - v_0^2 &=& 2ax \\
\\
\frac{1}{2} m \cdot v^2 - \frac{1}{2} m \cdot v_0^2 &=& \frac{1}{2} m \cdot 2ax \\
\\
\frac{1}{2} mv^2 - \frac{1}{2} mv_0^2 &=& max
\end{eqnarray*}
となる。運動方程式$ma=mg$より
\begin{eqnarray*}
\frac{1}{2} mv^2 - \frac{1}{2} mv_0^2 &=& mgx \\
\\
\frac{1}{2} mv^2(t) - \frac{1}{2} mv_0^2 &=& mgx \\
\end{eqnarray*}
となる。
初期条件$v(0)=v_0 =0 ,\ v(t) = v ,\ x(0)=x_0 ,\ x(t)=x$より
\begin{eqnarray*}
\frac{1}{2} mv^2(t) &=& mgx(t) \\
\\
\frac{1}{2} mv^2(t) +[- mgx(t)]&=& 0 \\
\\
\frac{1}{2} mv^2 + (-mgh ) &=& 0
\end{eqnarray*}
となる。