エネルギー保存則

エネルギー保存則

保存とは何か？

　エネルギー保存則の話をする前に、「保存」の意味について解説する。ここでの「保存する」とは「時間的に変化しない」という意味である。「時間に依らない量」であるという事である。
　さて、この「時間的に変化しない」という事を示すいくつかの方法を紹介しよう。

計算する

• 「具体的に代入してみたら定数」となるケース
• 「積分してみたら定数」となるケース

いずれも、「計算してみたら定数が導けた」というパターンである。

$t$で微分をしたら$0$になる

• その物理量を$t$で微分したら$0$になった。

「$t$で微分をして$0$になった」という事は、「微分する前の物理量は$t$に対して定数であるはず」という事になる。

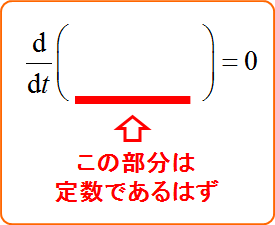
具体例を見ながら検討していく。

自由落下

　質量$m$の物体を地表から高さ$h$の地点から自由落下させる。このときのエネルギーについて検討せよ。

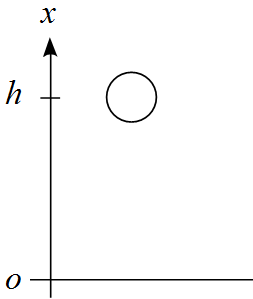
具体的に代入してみたら定数

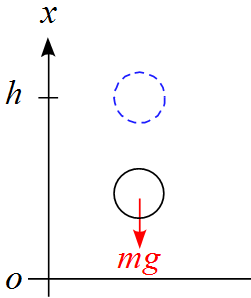
　運動方程式は
\begin{eqnarray*}
ma = -mg
\end{eqnarray*}
となる。

　速度$v(t)$は

\begin{eqnarray*}
a &=& -g \\
\\
\frac{\diff v}{\diff t} &=& -g \\
\\
\int \frac{\diff v}{\diff t} \diff t &=& \int ( -g) \diff t \\
\\
\int \diff v &=& \int (-g) \diff t \\
\\
v(t) &=& -gt +C
\end{eqnarray*}
となる。
自由落下なので$v(0)=0$であるから

\begin{eqnarray*}
v(0) = -g \cdot 0 +C &=& 0 \\
\\
C&=& 0
\end{eqnarray*}
となり、
\begin{eqnarray*}
v(t) = -gt
\end{eqnarray*}
となる。

また、物体の位置$x(t)$は

\begin{eqnarray*}
v(t) =\frac{\diff x}{\diff t} &=& -gt \\
\\
\int \frac{\diff x}{\diff t} \diff t &=& \int ( -gt) \diff t \\
\\
\int \diff x &=& \int (-gt) \diff t \\
\\
x(t) &=& - \frac{1}{2} gt^2 +C' \\
\end{eqnarray*}
となる。
初期条件は$x(0)=h$であるから

\begin{eqnarray*}
x(0) = - \frac{1}{2} g \cdot 0^2 +C' &=& h
\\
C' &=& h
\end{eqnarray*}
となり、
\begin{eqnarray*}
x(t) = -\frac{1}{2}gt^2 +h
\end{eqnarray*}
となる。

運動エネルギー$K(t)$は
\begin{eqnarray*}
K(t) &=& \frac{1}{2} mv^2(t) \\
\\
&=& \frac{1}{2} m (-gt)^2 \\
\\
&=& \frac{1}{2} m g^2 t^2
\end{eqnarray*}
となる。

重力による位置エネルギー$U(t)$
\begin{eqnarray*}
U(t) &=& mgx(t) \\
\\
&=& mg (-\frac{1}{2}gt^2 +h) \\
\\
&=& - \frac{1}{2} m g^2 t^2 + mgh
\end{eqnarray*}

従って、力学的エネルギー$E(t)$は
\begin{eqnarray*}
E(t) &=& K(t) +U (t) \\
\\
&=& \frac{1}{2} m g^2 t^2 + \left(- \frac{1}{2} m g^2 t^2 + mgh \right) \\
\\
&=& mgh
\end{eqnarray*}
となり、力学的エネルギー$E(t)$が一定値$mgh$となるので、エネルギー保存則が成り立っている。

積分してみたら定数

　運動方程式の両辺を$x$で積分すると

\begin{eqnarray*}
ma &=& - mg \\
\\
m \frac{\diff v}{\diff t} &=& - mg \\
\\
\int m \frac{\diff v}{\diff t} \diff x &=& \int ( - mg) \diff x \\
\\
\int m \frac{\diff v}{\diff t} v \diff t &=& \int ( - mg) \diff x \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t &=& \int (- mg) \diff x
\end{eqnarray*}
となる。

　ここで物体から手を放したした時刻を$t=0$とし、初期条件を$v(0) = v_0 =0 ,\ v(t) = v ,\ x(0) = h ,\ x(t) = x$とすると

\begin{eqnarray*}
\int \frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t &=& \int (- mg) \diff x \\
\\
\left[ \frac{1}{2} mv^2(t) \right]_{0}^{t} &=& [-mgx]_{h}^{x(t)} \\
\\
\frac{1}{2} mv^2(t) - \frac{1}{2} mv^2(0) &=& -mgx(t) - ( -mgh ) \\
\\
\frac{1}{2} mv^2 (t) - \frac{1}{2}m \cdot 0^2 &=& -mgx(t) + mgh \\
\\
\frac{1}{2} mv^2(t) +mgx(t) &=& mgh \\
\\
K(t) + U(t) &=& mgh \\
\\
E(t) &=& mgh
\end{eqnarray*}
となる。

　従って、運動エネルギ$K(t)$ と位置エネルギー$U(t)$の和である力学的エネルギー$E(t)$が一定値$mgh$となるので、エネルギー保存則が成り立っている。

$t$で微分をしたら$0$になる

　運動方程式を変形して$\displaystyle \frac{\diff }{\diff t}(\quad \quad )$の形を導く。

運動方程式の両辺に速度$v=\displaystyle \frac{\diff x}{\diff t}$をかけると

\begin{eqnarray*}
m \frac{\diff v}{\diff t} &=& - mg \\
\\
m \frac{\diff v}{\diff t} v &=& - mg \frac{\diff x}{\diff t} \\
\\
\frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 \right) &=& \frac{\diff }{\diff t} (-mgx) \\
\\
\frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 \right) + \frac{\diff }{\diff t} (mgx) &=& 0 \\
\\
\frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 +mgx \right) &=& 0 \\
\\
\frac{\diff}{\diff t} \left( K(t) +U(t) \right) &=& 0 \\
\\
\frac{\diff}{\diff t} \left( E(t) \right) &=& 0
\end{eqnarray*}
となる。

　よって、運動エネルギ$K(t)$ と位置エネルギー$U(t)$の和である力学的エネルギー$E(t)$を時間$t$で微分したものが$0$となるので、微分する前の量$E(t)$は時間に依らず一定である。
従って、エネルギー保存則が成り立っていると言える。

自由落下のエネルギー変化

$E-t$グラフ

　運動エネルギー$K(t)$, 重力による位置エネルギー$U(t)$, 力学的エネルギー$E(t)$は

\begin{eqnarray*}
K(t) &=& \frac{1}{2} m g^2 t^2 \\
\\
U(t) &=& - \frac{1}{2} m g^2 t^2 + mgh \\
\\
E(t) &=& mgh
\end{eqnarray*}
である。

これらを$E-t$グラフで表すと下図のようになる。

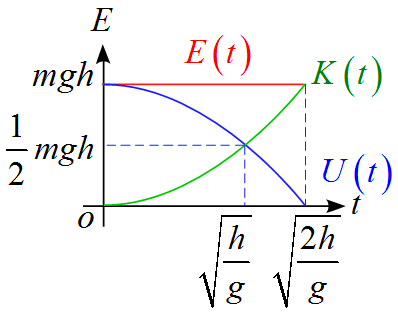
• $K(t)$は$t$の2次関数で下に凸のグラフである。
• $U(t)$は$t$の2次関数で上に凸のグラフである。

$K(t),\ U(t)$の交点は

\begin{eqnarray*}
\frac{1}{2} m g^2 t^2 &=& - \frac{1}{2} m g^2 t^2 + mgh \\
\\
m g^2 t^2 &=& mgh \\
\\
t^2 &=& \frac{h}{g} \\
\\
t &=& \sqrt{\frac{h}{g}}
\end{eqnarray*}
となる。