運動方程式を立てるには作図が重要であることは前回に述べた通りである。今回も引き続き物理モデルを解説していく。
今回は、動かない状態のモデルを取り上げた。動かないモデルの場合でもまずは運動方程式を立てるところから進めていく。立式した運動方程式において、加速度$a=0$の条件を適用すれば良い。
物体を3方向から引いた例
物体を水平面上で3方向に引いたモデルを考える。図は、物体を真上から見た図である。(重力は図の手前から奥に向かって作用しているとする。)
物体を3方向から引いた例のモデル図
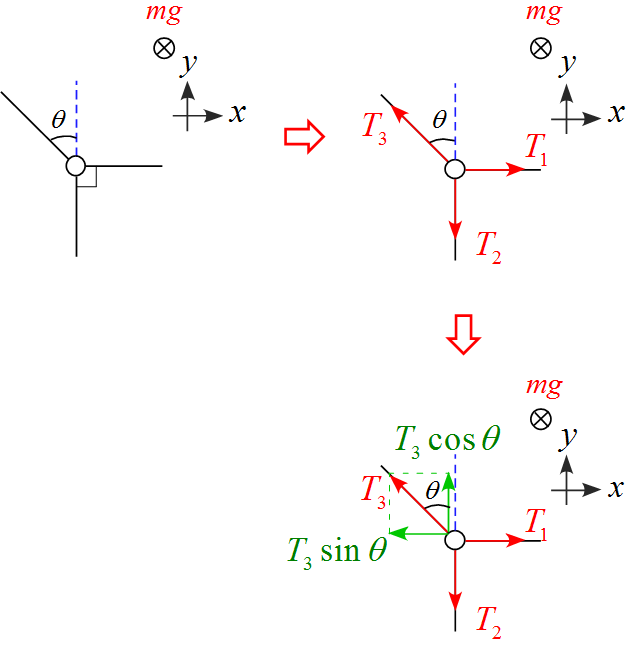
- 水平面上において右向きを$x$軸の正に、上向きを$y$軸の正と設定した。
- 水平面上において物体に作用する力は張力$T_1, \ T_2, \ T_3 \ $の3つである。
- 張力$T_3$を$x, \ y$ 軸に沿って分解すると$x$成分の大きさは「$T_3 \sin \theta$」、$y$成分の大きさは「$T_3 \cos \theta$」となる。
物体を3方向から引いた例の運動方程式
運動方程式は
\begin{eqnarray*}
m a_x &=& T_1 -T_3 \sin \theta \\
\\
m a_y &=& T_3 \cos \theta - T_2
\end{eqnarray*}
となる。
この状態で静止している(つり合っている)ならば、$a_x =0, \ a_y =0 $であり、
\begin{eqnarray*}
0 &=& T_1 -T_3 \sin \theta \\
\\
0 &=& T_3 \cos \theta - T_2
\end{eqnarray*}
より
\begin{eqnarray*}
T_1 &=& T_3 \sin \theta \\
\\
T_2 &=& T_3 \cos \theta
\end{eqnarray*}
となり、これは所謂「つり合い式」を表している。
天井から2本の糸でつるされた物体の例
天井から2本の糸で物体がつるされている。2つの糸と天井のなす角をそれぞれ下図のように$\alpha,\ \beta \ $とする。尚、天井と2本の糸で作られる三角形は直角三角形とは限らないので一般化した設定とした。
天井から2本の糸でつるされた物体の例のモデル図
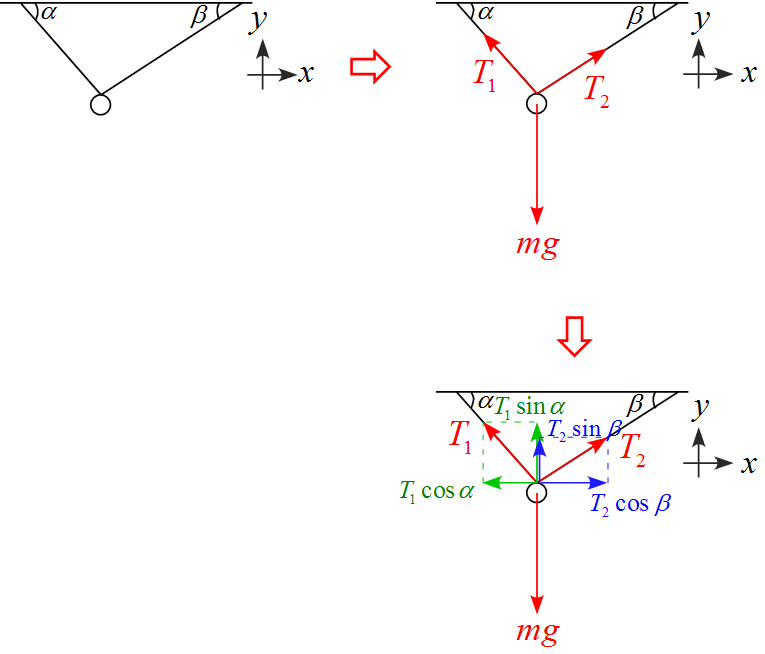
- 右向きを$x$軸の正に、上向きを$y$軸の正と設定した。
- 作用する力は重力$mg$, 糸の張力$T_1, \ T_2 \ $ の3つである。
- 張力$T_1$を$x, \ y$ 軸に沿って分解すると$x$成分の大きさは「$T_1 \cos \alpha$」、$y$成分の大きさは「$T_1 \sin \alpha$」となる。
- 張力$T_2$を$x, \ y$ 軸に沿って分解すると$x$成分の大きさは「$T_2 \cos \beta$」、$y$成分の大きさは「$T_2 \sin \beta$」となる。
天井から2本の糸でつるされた物体の例の運動方程式
運動方程式は
\begin{eqnarray*}
m a_x &=& T_2 \cos \beta -T_1 \cos \alpha \\
\\
m a_y &=& T_1 \sin \alpha + T_2 \sin \beta - mg
\end{eqnarray*}
となる。
この状態で静止している(つり合っている)ならば、$a_x =0, \ a_y =0 $であり、
\begin{eqnarray*}
0 &=& T_2 \cos \beta -T_1 \cos \alpha \\
\\
0 &=& T_1 \sin \alpha + T_2 \sin \beta - mg
\end{eqnarray*}
となる。
定滑車につるされた2物体の片方が地面にある例
定滑車に質量$m_A, \ m_B $の2つの物体がつるされ、片方が地面に置かれた状態である。
定滑車につるされた2物体の片方が地面にある例のモデル図
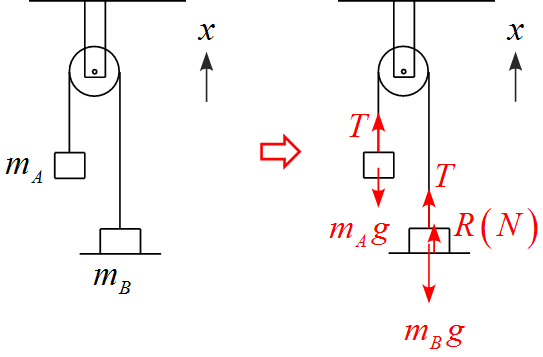
- $x$軸を上向きを正に設定した。
- 物体$A$に作用する力は重力$m_A$と糸の張力$T$の2つである。
- 物体$B$に作用する力は重力$m_B$, 面からの抗力$R(N)$, 糸の張力$T$の3つである。
定滑車につるされた2物体の片方が地面にある例の運動方程式
物体$A,\ B$のそれぞれの加速度を$a_A, \ a_B$とすると
運動方程式は物体$A$について
\begin{eqnarray*}
m a_A = T - m_A g
\end{eqnarray*}
物体$B$について
\begin{eqnarray*}
m a_B = T - m_B g + N
\end{eqnarray*}
となる。
この状態で静止しているならば束縛条件は$a_A =0, \ a_B =0 $であり、
\begin{eqnarray*}
0 &=& T - m_A g \\
\\
0 &=& T - m_B g + N
\end{eqnarray*}
より、糸の張力$T$は
\begin{eqnarray*}
T &=& m_A g
\end{eqnarray*}
となり、垂直抗力$N$は
\begin{eqnarray*}
N &=& m_B g - T \\
\\
&=& m_B g - m_A g \\
\\
&=& (m_B - m_A)g
\end{eqnarray*}
となる。