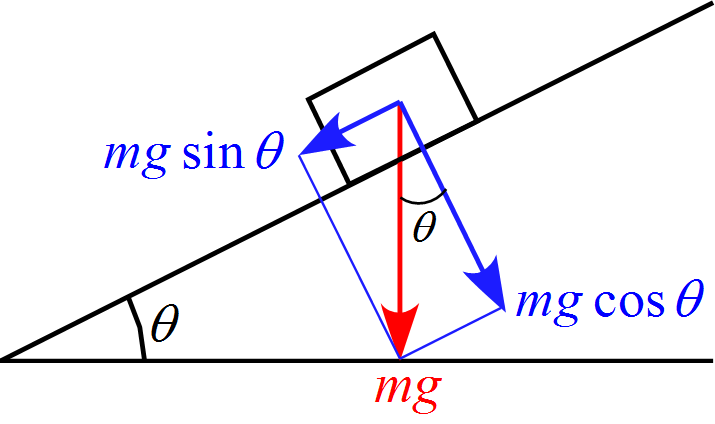
斜面を滑るモデルを考える場合、斜面に沿った軸と斜面に垂直な軸を設定し考える。
当然、重力$mg$は真下に向くので、重力$mg$を軸に沿った形に成分を分解する必要がある。
さて、水平面と斜面とのなす角$\theta$はどの部分になるだろうか?
この機会に、しっかりと確認をしておこう。
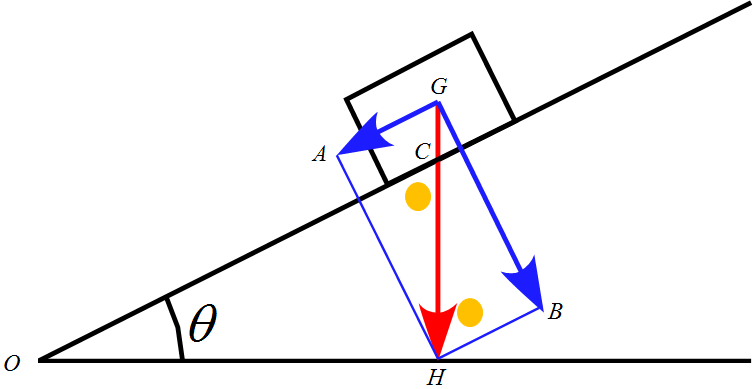
$\theta$でない角に着目しすると、$\text{OC} \parallel \text{HB}$より
\begin{eqnarray*}
\angle \text{OCH} = \angle \text{GHB} \ \ (錯角)
\end{eqnarray*}
ここで $\triangle{\text{OCH}}$ において
\begin{eqnarray*}
\angle \text{COH} + \angle \text{OCH} =90^{\circ}
\end{eqnarray*}
また、$\triangle{\text{GHB}}$ において
\begin{eqnarray*}
\angle \text{HGB} + \angle \text{GHB} =90^{\circ}
\end{eqnarray*}
従って
\begin{eqnarray*}
\angle \text{COH} = \angle \text{HGB} =\theta
\end{eqnarray*}
となる。
よって、重力$mg$は下図の様に成分を分解することができる。