力のモーメントの例題を再検討する

力のモーメントの例題を再検討する

　前回の解説を踏まえて前回の例題を再検討する。　

力のモーメントの定義からわかること

　前回の定義より

である。この式から考えると力のモーメント$\vec{M}$の大きさは

\begin{eqnarray*}
| \vec{M} | = |\vec{r}||\vec{F}| \sin \theta
\end{eqnarray*}
となると言える。
ここで、角$\theta$は位置ベクトル$\vec{r}$と作用する力$\vec{F}$のなす角である。
従って、$\sin \theta$はなす角が$\theta=0$であれば$\sin 0 =0 $となり力のモーメント$\vec{M}$の大きさは$0$になり、なす角が$\theta = 90^\circ$であれば$\sin 90^\circ =1$となり力のモーメント$\vec{M}$の大きさは$|\vec{r}||\vec{F}|$となる。

　つまり、力のモーメントを考えるときに「直行する成分だけを考える」と学校で言われたことのもとになる部分である。

前回の例題

　さて、実際に例題を見てみよう。まず、位置ベクトルと作用する力を設定する。左側と右側にそれぞれ添字を$\text{A}$とし、座標軸を下図のように設定すると

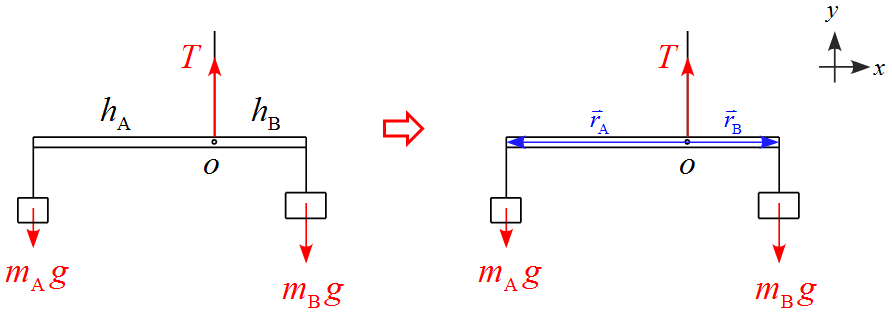
位置ベクトルは
\begin{eqnarray*}
\vec{r}_{\text{A}} &=&
\begin{pmatrix}
-h_{\text{A}} \\
0 \\
0 \\
\end{pmatrix} \\
\\
\vec{r}_{\text{B}} &=&
\begin{pmatrix}
h_{\text{B}} \\
0 \\
0\\
\end{pmatrix}
\end{eqnarray*}

である。
また、作用する力は

\begin{eqnarray*}
\vec{F}_{\text{A}} &=&
\begin{pmatrix}
0\\
-m_{\text{A}} g \\
0 \\
\end{pmatrix} \\
\\
\vec{F}_B &=&
\begin{pmatrix}
0 \\
-m_{\text{B}} g \\
0\\
\end{pmatrix}
\end{eqnarray*}

である。

従って
\begin{eqnarray*}
| \vec{M}_{\text{A}} | &=& |\vec{r}_{\text{A}}||\vec{F}_{\text{A}}| \sin \theta_{\text{A}} \\
\\
&=& \sqrt{(-h_{\text{A}})^2 +0^2 + 0^2} \cdot \sqrt{0^2 +(-m_{\text{A}} g)^2 +0^2} \sin 90^\circ \\
\\
&=& h_{\text{A}} m_{\text{A}} g
\end{eqnarray*}
となり

\begin{eqnarray*}
| \vec{M}_{\text{B}} | &=& |\vec{r}_{\text{B}}||\vec{F}_{\text{B}}| \sin \theta_{\text{B}} \\
\\
&=& \sqrt{(h_{\text{B}})^2 +0^2 + 0^2} \cdot \sqrt{0^2 +(-m_{\text{B}} g)^2 +0^2} \sin (-90^\circ) \\
\\
&=& -h_{\text{B}} m_{\text{B}} g
\end{eqnarray*}
となる。ここで$\text{B}$についてのマイナスは向きが逆という意味である。物理では一般的に反時計回りを正に取るので回転方向によって正負が決まることになる。

　これらが前回の「反時計回りの力モーメント」と「時計回りの力のモーメント」に相当する値である。

実際に外積を計算する

　さらに深堀りをして、このベクトルの外積を計算してみよう。外積の定義より、それぞれの成分計算は

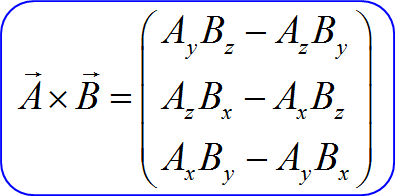
であるから、

\begin{eqnarray*}
\vec{M}_{\text{A}} &=& \vec{r}_{\text{A}} \times \vec{F}_{\text{A}} \\
\\
&=&
\begin{pmatrix}
-h_{\text{A}} \\
0 \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
0\\
-m_{\text{A}} g\\
0\\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \cdot 0 -0 \cdot (- m_{\text{A}} g) \\
0 \cdot 0 - (- h_{\text{A}}) \cdot 0\\
(-h_{\text{A}})(-m_{\text{A}} g) - 0 \cdot 0 \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
h_{\text{A}}m_{\text{A}} g \\
\end{pmatrix}\\
\end{eqnarray*}

となり、

\begin{eqnarray*}
\vec{M}_{\text{B}} &=& \vec{r}_{\text{B}} \times \vec{F}_{\text{B}} \\
\\
&=&
\begin{pmatrix}
h_{\text{B}} \\
0 \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
0\\
-m_{\text{B}} g\\
0\\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \cdot 0 -0 \cdot (- m_{\text{B}} g) \\
0 \cdot 0 - h_{\text{B}} \cdot 0\\
h_{\text{B}} (-m_{\text{B}} g) - 0 \cdot 0 \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
-h_{\text{B}}m_{\text{B}} g \\
\end{pmatrix}\\
\end{eqnarray*}

となる。

回転の運動方程式$\displaystyle \frac{\diff \vec{L}}{\diff t} = \vec{M}$より

\begin{eqnarray*}
\frac{\diff \vec{L}}{\diff t} &=& \vec{M} \\
\\
&=& \vec{M}_{\text{A}} + \vec{M}_{\text{B}} \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
h_{\text{A}}m_{\text{A}} g \\
\end{pmatrix} +
\begin{pmatrix}
0 \\
0 \\
-h_{\text{B}}m_{\text{B}} g \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
h_{\text{A}}m_{\text{A}} g -h_{\text{B}}m_{\text{B}} g\\
\end{pmatrix}\\
\\
\begin{pmatrix}
\frac{\diff L_x}{\diff t} \\
\frac{\diff L_y}{\diff t} \\
\frac{\diff L_z}{\diff t} \\
\end{pmatrix}
&=&
\begin{pmatrix}
0 \\
0 \\
h_{\text{A}}m_{\text{A}} g -h_{\text{B}}m_{\text{B}} g\\
\end{pmatrix}\\
\end{eqnarray*}

となる。成分を見る通り、$z$成分だけ考えれば良いことがわかる。

従って、回転しない条件は

\begin{eqnarray*}
\frac{\diff L_z}{\diff t} =h_{\text{A}}m_{\text{A}} g -h_{\text{B}}m_{\text{B}} g =0
\end{eqnarray*}

となる。

まとめ

• 位置ベクトル$\vec{r}$と作用する力$\vec{F}$をきちんと設定する
• 位置ベクトル$\vec{r}$と作用する力$\vec{F}$とのなす角$\theta$は図から理解できる。
• 力のモーメント$\vec{M}$はベクトル量である。教科書で書かれている量は大きさとして考えていることに注意する。
• 実際にベクトルの外積を計算すると、外積の性質より$z$成分だけ考えれば良いことが言える