力のモーメント ~ 練習問題 part-1
今回は力のモーメントに関連した基礎的な練習問題を取り上げる。

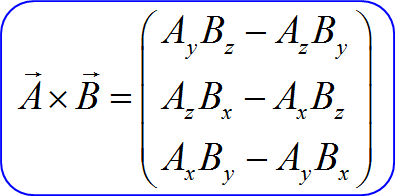
力のモーメントを求める
質量が無視できる棒の右端に力$F$を作用させた。力のモーメントを計算せよ。
左端を支点として、力の作用点までの位置ベクトル$\vec{r}$を設定する。
(1) 棒と垂直に力$\vec{F}$を作用させた。

位置ベクトル$\vec{r}$は
\begin{eqnarray*}
\vec{r} &=&
\begin{pmatrix}
x \\
0 \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}
である。
作用する力$\vec{F}$は
\begin{eqnarray*}
\vec{F} &=&
\begin{pmatrix}
0 \\
F \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}
である。
教科書的計算
力のモーメント$\vec{M}$の大きさは
\begin{eqnarray*}
| \vec{M} | = |\vec{r}||\vec{F}| \sin \theta
\end{eqnarray*}
より
\begin{eqnarray*}
| \vec{M} | &=& |\vec{r}||\vec{F}| \sin \theta \\
\\
&=& x \cdot F \sin 90^{\circ} \\
\\
&=& xF
\end{eqnarray*}
外積を使って計算
力のモーメント$\vec{M}$は
\begin{eqnarray*}
\vec{M} = \vec{r} \times \vec{F} &=&
\begin{pmatrix}
x \\
0 \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
0 \\
F \\
0 \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
0 \cdot 0 - 0 \cdot F \\
0 \cdot 0 - x \cdot 0 \\
x \cdot F - 0 \cdot 0 \\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
xF \\
\end{pmatrix}
\end{eqnarray*}
力のモーメントの大きさは
\begin{eqnarray*}
M = |\vec{M}| = \sqrt{0^2 + 0^2 + (xF)^2} =xF
\end{eqnarray*}
となる。
(2) 棒となす角$\theta$で力$\vec{F}$を作用させた。
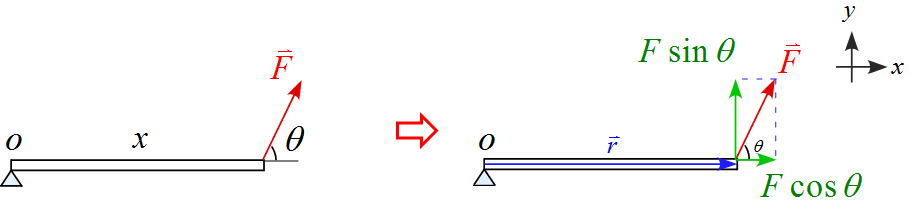
位置ベクトル$\vec{r}$は
\begin{eqnarray*}
\vec{r} &=&
\begin{pmatrix}
x \\
0 \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}
である。
作用する力$\vec{F}$は
\begin{eqnarray*}
\vec{F} &=&
\begin{pmatrix}
F \cos \theta \\
F \sin \theta \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}
である。
教科書的計算
力のモーメント$\vec{M}$の大きさは
\begin{eqnarray*}
| \vec{M} | = |\vec{r}||\vec{F}| \sin \theta
\end{eqnarray*}
より
\begin{eqnarray*}
| \vec{M} | &=& |\vec{r}||\vec{F}| \sin \theta \\
\\
&=& x \cdot F \sin \theta \\
\\
&=& xF \sin \theta
\end{eqnarray*}
外積を使って計算
力のモーメント$\vec{M}$は
\begin{eqnarray*}
\vec{M} = \vec{r} \times \vec{F} &=&
\begin{pmatrix}
x \\
0 \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
F \cos \theta \\
F \sin \theta \\
0 \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
0 \cdot 0 - 0 \cdot F \sin \theta \\
0 \cdot F \cos \theta - x \cdot 0 \\
x \cdot F \sin \theta - 0 \cdot F \cos \theta \\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
xF \sin \theta \\
\end{pmatrix}
\end{eqnarray*}
力のモーメントの大きさは
\begin{eqnarray*}
M = |\vec{M}| = \sqrt{0^2 + 0^2 + (xF \sin \theta)^2} =xF \sin \theta
\end{eqnarray*}
となる。
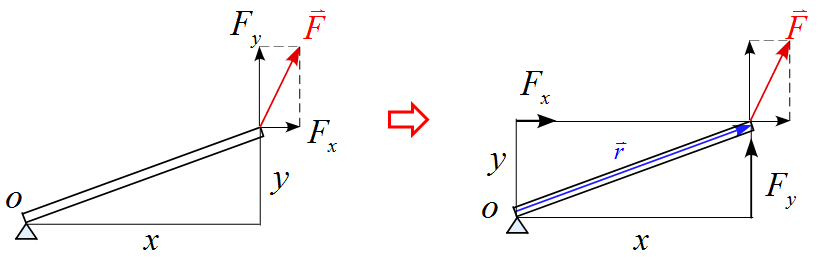
(3) 下図の様に斜めになった状態の棒に力$\vec{F}$を作用させた。
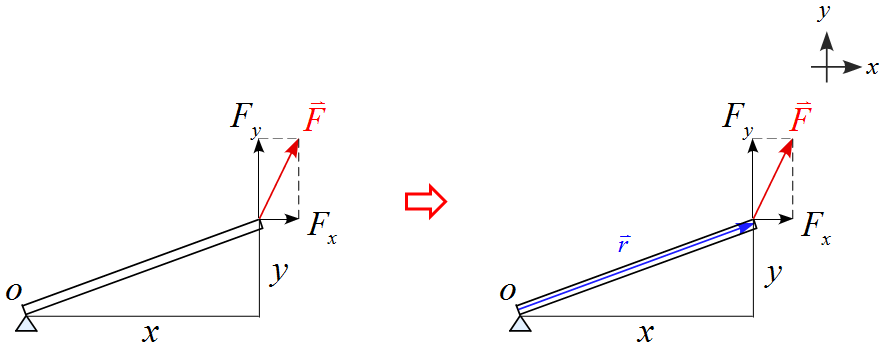
位置ベクトル$\vec{r}$は
\begin{eqnarray*}
\vec{r} &=&
\begin{pmatrix}
x \\
y \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}
である。
作用する力$\vec{F}$は
\begin{eqnarray*}
\vec{F} &=&
\begin{pmatrix}
F_x \\
F_y \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}
である。
教科書的計算
力のモーメント$\vec{M}$の大きさは
\begin{eqnarray*}
| \vec{M} | = |\vec{r}||\vec{F}| \sin \theta
\end{eqnarray*}
であるが、位置ベクトル$\vec{r}$と作用する力$\vec{F}$のなす角が与えられていないのでこのまま計算することは困難である。
外積を使って計算
力のモーメント$\vec{M}$は
\begin{eqnarray*}
\vec{M} = \vec{r} \times \vec{F} &=&
\begin{pmatrix}
x \\
y \\
0 \\
\end{pmatrix} \times
\begin{pmatrix}
F_x \\
F_y \\
0 \\
\end{pmatrix}\\
\\
&=&
\begin{pmatrix}
y \cdot 0 - 0 \cdot F_y \\
0 \cdot F_x - x \cdot 0 \\
x \cdot F_y - y \cdot F_x \\
\end{pmatrix} \\
\\
&=&
\begin{pmatrix}
0 \\
0 \\
xF_y - yF_x \\
\end{pmatrix}
\end{eqnarray*}
力のモーメントの大きさは
\begin{eqnarray*}
M = |\vec{M}| = \sqrt{0^2 + 0^2 + (xF_y - yF_x)^2} =xF_y - yF_x
\end{eqnarray*}
となる。
さて、ここで力のモーメント$\vec{M}$の$z$成分を見てみると、これは位置ベクトル$\vec{r}$を$x,y$成分に分けて力が作用したとみなしたものに相当する。
\begin{eqnarray*}
\text{反時計回りの力のモーメント} &=&x F_y\\
\\
\text{時計回りの力のモーメント} &=& y F_x \\
\end{eqnarray*}
であるから、力のモーメント$\vec{M}$の大きさは
\begin{eqnarray*}
M = x F_y -y F_x
\end{eqnarray*}
となる。