仕事とエネルギー ~ 練習問題 part-6

仕事とエネルギー ~ 練習問題 part-6

振り子の運動のエネルギー

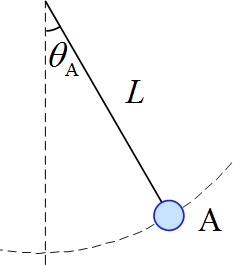
　長さ$L$の糸の一端を天井に取り付け、他端に質量$m$の物体をつるす。図のように糸が鉛直線となす角$\theta_{\text{A}}$の位置$\text{A}$から物体を静かに放した。
この運動で糸はたるまないものとして考えよ。

(1) 張力$T$のした仕事$W_T$を求めよ。

(2) 最下点での物体の速度を求めよ。

解答

軸を設定し、作用する力を書き込む

• $x$軸の正の向きは右側に、$y$軸の正の向きは上に設定した。
• 作用する力は重力$mg , \ $糸の張力$T ,\ $の2つである。
• 運動途中の角度を$\theta$と表した。
• 円運動なので極座標を用いるのが通常であるが、今回は直交座標系を用いる。

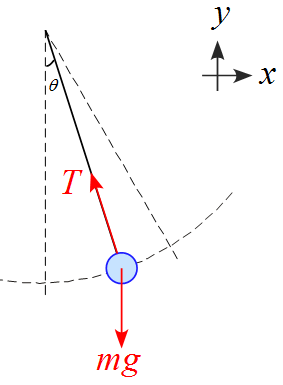
$x,y$軸に沿った成分に分解すると

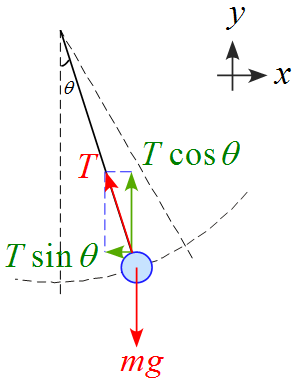
運動方程式を立てる

　運動方程式は
\begin{eqnarray*}
m a_x &=& - T \sin \theta \\
\\
m a_y &=& T \cos \theta - mg
\end{eqnarray*}
となる。

　ここで、運動方程式をベクトル表記に書き換えると、

\begin{eqnarray*}
m \vec{a} &=& \vec{F} \\
\\ m
\begin{pmatrix}
a_x \\
a_y \\
\end{pmatrix} &=&
\begin{pmatrix}
F_x \\
F_y \\
\end{pmatrix}\\
\\ m
\begin{pmatrix}
a_x \\
a_y \\
\end{pmatrix} &=&
\begin{pmatrix}
- T \sin \theta \\
T \cos \theta - mg \\
\end{pmatrix}
\end{eqnarray*}
となる。

仕事を計算する ~ 両辺を$\diff \vec{r}$で積分する

　両辺を$\diff \vec{r}$の内積を取って全体を積分すると

\begin{eqnarray*}
m \vec{a} &=& \vec{F} \\
\\
\int m\frac{\diff \vec{v}}{\diff t} \cdot \diff \vec{r} &=& \int \vec{F} \cdot \diff \vec{r} \\
\\
\int m\frac{\diff \vec{v}}{\diff t} \cdot \vec{v} \diff t &=& \int \vec{F} \cdot \diff \vec{r} \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t &=& \int \vec{F} \cdot \diff \vec{r} \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t
&=& \int
\begin{pmatrix}
F_x \\
F_y \\
\end{pmatrix} \cdot
\begin{pmatrix}
\diff x \\
\diff y \\
\end{pmatrix} \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t
&=& \int F_x \diff x + \int F_y \diff y \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t
&=& \int (- T \sin \theta) \diff x + \int (T \cos \theta - mg) \diff y \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t
&=& \int (- T \sin \theta) \diff x + \int T \cos \theta \diff y + \int (-mg) \diff y
\end{eqnarray*}

となる。

　ここで、変位$\diff \vec{r}$の位置関係は下図のようになる。

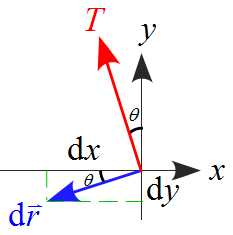
　よって、

\begin{eqnarray*}
\tan \theta &=& \frac{\diff y}{\diff x} \\
\\
\diff x &=& \frac{\diff y}{\tan \theta}
\end{eqnarray*}
であるから、張力$T$のする仕事は

\begin{eqnarray*}
W_T &=& W_{T_x} +W_{T_y} \\
\\
&=& \int (- T \sin \theta) \diff x + \int T \cos \theta \diff y \\
\\
&=& \int (- T \sin \theta) \cdot \frac{\diff y}{\tan \theta} + \int T \cos \theta \diff y \\
\\
&=& \int (- T \sin \theta) \cdot \frac{ \cos \theta}{\sin \theta}\ \diff y+ \int T \cos \theta \diff y \\
\\
&=& \int (- T \cos \theta) \diff y +\int T \cos \theta \diff y \\
\\
&=& 0
\end{eqnarray*}
となる。
　つまり、張力$T$については、張力$\vec{T}$と変位$\diff \vec{r}$のなす角は常に$90^{\circ}$であるから仕事はしないという事が確認できたことになる。

従って、仕事とエネルギーの関係式は

\begin{eqnarray*}
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff \vec{t}
&=& \int (- T \sin \theta) \diff x + \int T \cos \theta \diff y + \int (-mg) \diff y　\\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff \vec{t} &=& \int (-mg) \diff y
\end{eqnarray*}
となる。

　ここで初期条件は下図より$v(0) = v_0 =0 ,\ x(0) = L \sin \theta_{\text{A}} ,\ y(0) = L-L \cos \theta_{\text{A}}$とすると

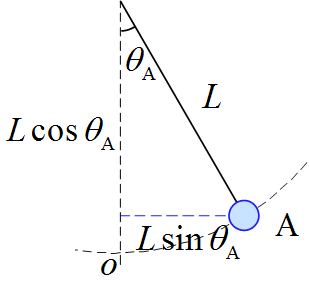
• 最下点を原点と設定した。

最下点に達する時刻を$t_1$とすると

\begin{eqnarray*}
\int_{0}^{t_1} \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff \vec{t} &=& \int_{L-L \cos \theta_{\text{A}}}^{0} (-mg) \diff y \\
\\
\left[ \frac{1}{2}mv^2(t) \right]_{0}^{t_1} &=& \left[ -mgx \right]_{L-L \cos \theta_{\text{A}}}^{0} \\
\\
\frac{1}{2}mv^2(t_1) -\frac{1}{2}mv^2(0) &=& -mg \cdot 0 - [ -mg (L-L \cos \theta_{\text{A}}) ] \\
\\
\frac{1}{2}mv^2(t_1) -\frac{1}{2}m \cdot 0^2 &=& mg (L-L \cos \theta_{\text{A}}) \\
\\
\frac{1}{2}mv^2(t_1) &=& mgL (1- \cos \theta_{\text{A}})
\end{eqnarray*}
となる。

よって、最下点での速度$v(t_1)$は

\begin{eqnarray*}
\frac{1}{2}mv^2(t_1) &=& mgL (1- \cos \theta_{\text{A}}) \\
\\
v^2(t_1) &=& 2gL (1- \cos \theta_{\text{A}}) \\
\\
v(t_1) &=& \sqrt{2gL (1- \cos \theta_{\text{A}})}
\end{eqnarray*}
となる。但し、速度$v(t_1)$は左向きである。

教科書的計算

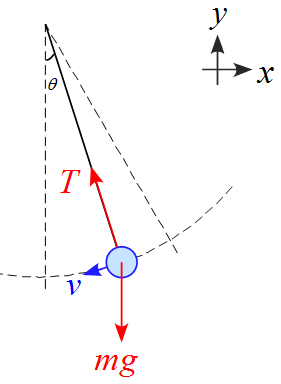
　物体の動く向き$v$と張力$T$は垂直なので仕事はしない。
従って、
\begin{eqnarray*}
W_T = 0
\end{eqnarray*}
となる。

　エネルギー保存則より

\begin{eqnarray*}
\frac{1}{2}mv^2(0) + mg (L - L \cos \theta_{\text{A}}) &=& \frac{1}{2}mv^2(t_1) + mg \cdot 0 \\
\\
\frac{1}{2}mv^2(t_1) &=& mgL (1- \cos \theta_{\text{A}}) \\
\\
v^2(t_1) &=& 2gL (1- \cos \theta_{\text{A}}) \\
\\
v(t_1) &=& \sqrt{2gL (1- \cos \theta_{\text{A}})}
\end{eqnarray*}

となる。但し、速度$v(t_1)$は左向きである。