加速度と$v-t$グラフ
前回は加速度の一般的な定義の解説をした。今回は加速度と$v-t$グラフについて直線(1次元)の運動を用いて解説していく。
直線(1次元)運動
前回は3次元の一般的な運動を扱ったが、ここでは1次元の運動について考える。
ある時刻$t$で点$\text{P}$の位置に居た物体が、時刻$t+ \Delta t$には点$\text{P'}$に居たとする。このとき、速度が$\vec{v}$から$\vec{v} + \Delta \vec{v}$に変化したとする。
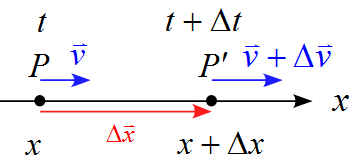
$v-t$グラフ
$x-t$グラフで表すと下図のようになる。
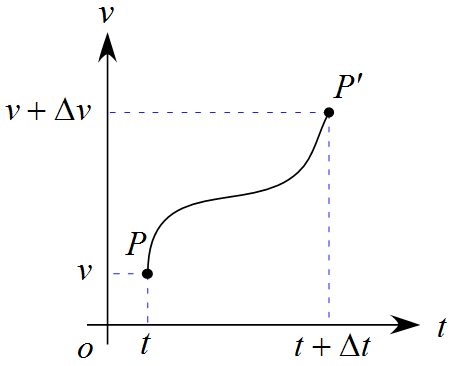
点$\text{P}$から点$\text{P}'$まで移動している間、加速度が一定とは限らないので曲線で表している。
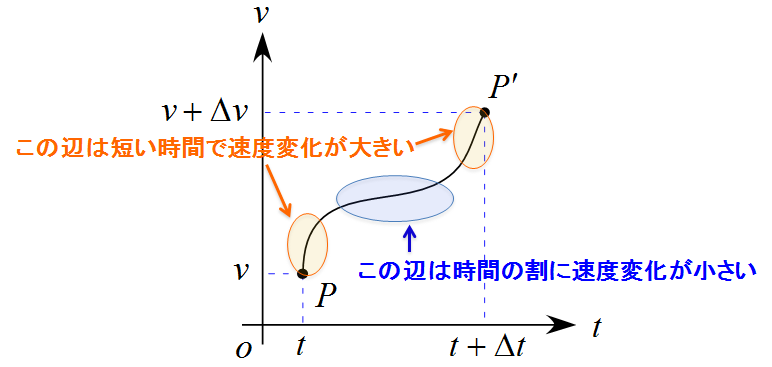
この$v-t$グラフを見てみると、点$\text{P}$の付近と点$\text{P}'$の付近が急勾配で、中間付近はなだらかになっていることがわかる。
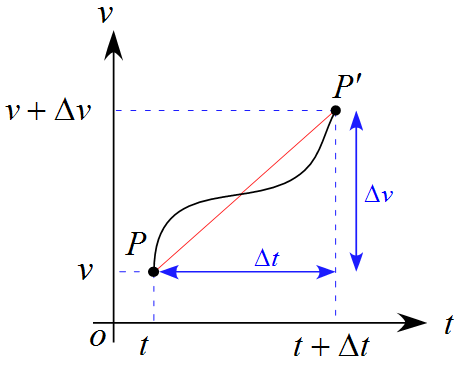
平均の加速度$\bar{a}$
傾きが急な部分もなだらかな部分もあるが、平均するとどうなるかを考えたものが「平均の加速度」となる。
速度の定義から考えると、
\begin{eqnarray*}
\vec{a} = \frac{\diff \vec{v}}{\diff t} =
\begin{pmatrix}
\frac{\diff v_x}{\diff t} \\
\frac{\diff v_y}{\diff t} \\
\frac{\diff v_z}{\diff t} \\
\end{pmatrix} =
\begin{pmatrix}
a_x \\
a_y \\
a_z \\
\end{pmatrix}
\end{eqnarray*}
即ち
\begin{eqnarray*}
a_x=\frac{\diff v_x}{\diff t}
\end{eqnarray*}
であるから、$a_x$は$v-t$グラフの傾きを求めることになり、
\begin{eqnarray*}
\bar{a} = \frac{\Delta v_x}{\Delta t} \ \quad \text{(平均の加速度)}
\end{eqnarray*}
となる。
瞬間の加速度$a_x$
点$\text{P}$から点$\text{P}'$まで移動している間の点$\text{C}$を考える。この点$\text{C}$の位置を$x$, 時刻$t$ とし、そこから微笑時間$\Delta t$後に微小の速度変化の大きさが$\Delta v$とする。
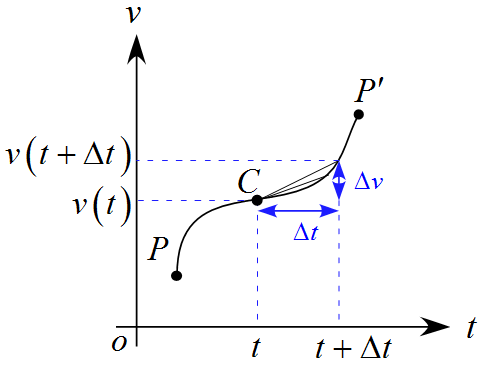
ここで、この微小時間$\Delta t$を限りなく小さくしてく、即ち$\Delta t \to 0$ の極限を考えるとこの傾きはこの曲線の接線となり、
\begin{eqnarray*}
\lim_{\Delta t \to 0} \frac{\Delta v}{\Delta t} = \lim_{\Delta t \to 0} \frac{v(t+\Delta t) - v(t)}{\Delta t} =\frac{\diff v}{\diff t}
\end{eqnarray*}
となる。
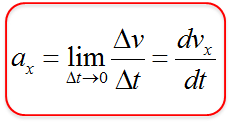
加速度の大きさ$a<0$とはどういう状態か?
加速度$a$が$a>0$の状態であれば、加速するということ解るだろう。では加速度$a$が$a<0$とはどういう状態であるか、下図の$v-t$グラフを見ながら考えてみよう。
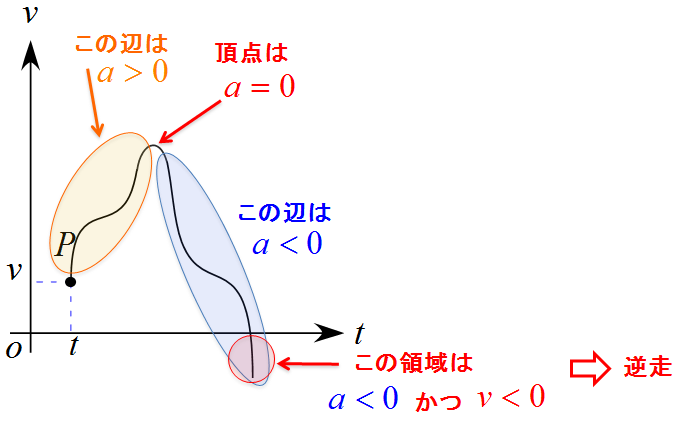
点$\text{P}$を出発して$v-t$グラフの頂点までは$a>0$であり、加速している状態で、速度$v$が増えている状態である。頂点を超えてからは$a<0$となり、減速している状態で、速度$v$が減っていく状態である。さらに、速度$v$が減っていき$v<0$となる事態が起こる。ここでの速度が$v<0$と言う意味は逆走すると言うことになる。「加速度$a<0$だからといって必ずしも逆走しているわけではない」ことに注意したい。