速度に比例した空気抵抗がある物体の落下の微分方程式を解く
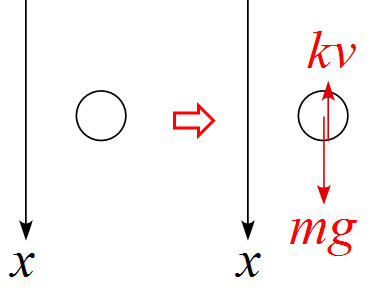
「前回にやった速度に比例した空気抵抗がある物体の運動方程式」
\begin{eqnarray*}
m \frac{\diff v}{\diff t} =mg-kv
\end{eqnarray*}
を解く
$v - \frac{mg}{k}$を別の文字で一旦置いて解く
\begin{eqnarray*}
m \frac{\diff v}{\diff t} &=& mg-kv \\
\\
m \frac{\diff v}{\diff t} &=& -kv -mg \\
\\
m \frac{\diff v}{\diff t} &=& -k \left( v - \frac{mg}{k} \right) \\
\\
\frac{\diff v}{\diff t} &=& -\frac{k}{m} \left( v - \frac{mg}{k} \right) \ \ \cdots (A) \\
\end{eqnarray*}
となる。ここで右辺の括弧の部分$\left( v - \frac{mg}{k} \right)$を$V$と置くと
\begin{eqnarray*}
V &=& \left( v - \frac{mg}{k} \right) \\
\\
\frac{\diff V}{\diff t} &=& \frac{\diff }{\diff t} \left( v - \frac{mg}{k} \right) = \frac{\diff v}{\diff t} \\
\\
\end{eqnarray*}
であるから、$v$を$V$へ置き換えると式$(A)$は、
\begin{eqnarray*}
\frac{\diff V}{\diff t} &=& -\frac{k}{m} V \\
\\
\frac{\diff V}{V} &=& -\frac{k}{m} \diff t \ \ \ \ \text{(変数分離)} \\
\\
\int \frac{\diff V}{V} &=& \int \left( -\frac{k}{m} \right) \diff t
\\
\\
\log |V| &=& -\frac{k}{m} t +C \\
\\
V &=& \pm e^{-\frac{k}{m} t +C} \\
\\
V &=& \pm e^{C} \cdot e^{-\frac{k}{m} t} \\
\\
V &=& C' \cdot e^{-\frac{k}{m} t} \\
\end{eqnarray*}
ここで置き換えていた部分を元に戻すと、
\begin{eqnarray*}
v - \frac{mg}{k} &=& C' \cdot e^{-\frac{k}{m} t} \\
\\
v &=& C' \cdot e^{-\frac{k}{m} t} + \frac{mg}{k} \\
\end{eqnarray*}
となる。
初期条件を$v(0)=0$とすると
\begin{eqnarray*}
v (0) = C' \cdot e^{-\frac{k}{m} \cdot 0} + \frac{mg}{k} &=& 0 \\
\\
C' + \frac{mg}{k} &=& 0 \\
\\
C' &=& - \frac{mg}{k}
\end{eqnarray*}
であるから、求める速度$v(t)$は
\begin{eqnarray*}
v (t) &=& -\frac{mg}{k} e^{-\frac{k}{m}t} + \frac{mg}{k} \\
\\
&=& \frac{mg}{k} \left( 1- e^{-\frac{k}{m}t} \right)
\end{eqnarray*}
となる。
別の文字で置かずに一気に解く
\begin{eqnarray*}
m \frac{\diff v}{\diff t} &=& mg-kv \\
\\
m \frac{\diff v}{\diff t} &=& -kv -mg \\
\\
m \frac{\diff v}{\diff t} &=& -k \left( v - \frac{mg}{k} \right) \\
\\
\frac{\diff v}{\diff t} &=& -\frac{k}{m} \left( v - \frac{mg}{k} \right) \\
\\
\frac{\diff v}{\diff t} \frac{1}{v - \frac{mg}{k}} &=& -\frac{k}{m} \left( v - \frac{mg}{k} \right) \frac{1}{v - \frac{mg}{k}} \\
\\
\frac{1}{v - \frac{mg}{k}} \frac{\diff v}{\diff t} &=& -\frac{k}{m} \\
\\
\frac{1}{v - \frac{mg}{k}} \diff v &=& -\frac{k}{m} {\diff t} \\
\\
\int \frac{1}{v - \frac{mg}{k}} \diff v &=& \int \left( -\frac{k}{m} \right) {\diff t} \\
\\
\log | v - \frac{mg}{k} | &=& -\frac{k}{m} t + C_1 \\
\\
v - \frac{mg}{k} &=& \pm e^{ -\frac{k}{m} t + C_1} \\
\\
v - \frac{mg}{k} &=& \pm e^{C_1} \cdot e^{-\frac{k}{m}t} \\
\\
v - \frac{mg}{k} &=& C_2 \cdot e^{-\frac{k}{m}t} \\
\\
v &=& C_2 \cdot e^{-\frac{k}{m}t} + \frac{mg}{k} \\
\end{eqnarray*}
となる。
初期条件を$v(0)=0$とすると
\begin{eqnarray*}
v (0) = C_2 \cdot e^{-\frac{k}{m} \cdot 0} + \frac{mg}{k} &=& 0 \\
\\
C_2 + \frac{mg}{k} &=& 0 \\
\\
C_2 &=& - \frac{mg}{k}
\end{eqnarray*}
であるから、求める速度$v(t)$は
\begin{eqnarray*}
v (t) &=& -\frac{mg}{k} e^{-\frac{k}{m}t} + \frac{mg}{k} \\
\\
&=& \frac{mg}{k} \left( 1- e^{-\frac{k}{m}t} \right)
\end{eqnarray*}
となる。
- 変数分離は微分方程式の解法の基本の一つです。手順を踏んで計算すれば複雑な計算では無いです。
- 高校物理の範囲ではグラフの概形が理解できていればよい。
- 大学生以上は微分方程式も自力で解けるようにするべきである。