速度・加速度まとめ

速度・加速度まとめ

投稿日：2019年11月23日

　今回は速度・加速度のまとめについて解説する。直線運動に絞って解説をするが、速度 $\vec{v}$ も加速度 $\vec{a}$ もそれぞれ各成分は独立して考えることができる。従って、平面運動や空間運動でも拡張して同様に考えることができることを付け加えておく。

速度

　速度の定義を理解するには $x-t$ グラフは欠かせない。速度は「時間に対する変位の変化率」である。
　下図のような $x-t$ グラフを考え、点 $\text{P}$ から点 $\text{P'}$ までの移動中のある点 $\text{C}$ を考える。

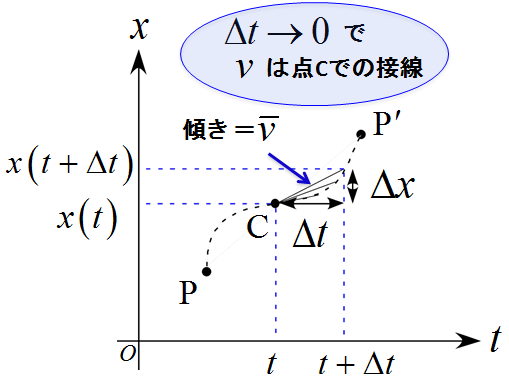
　ここで点 $\text{C}$ を通過する時刻 $t$ から時間 $\Delta t$ 後までの変位 $\Delta x$ は

$\begin{eqnarray*} \Delta x = x(t+\Delta t) - x(t) \end{eqnarray*}$

と表される。
　従って、「時間 $\Delta t$ に対する変位 $\Delta x$ の変化率」は

$\begin{eqnarray*} \text{変化率} = \frac{\Delta x}{\Delta t} = \frac{x(t+\Delta t) - x(t)}{\Delta t} \end{eqnarray*}$

である。これを「平均の速度 $\bar{v}$ 」と呼ぶ。

この「変化率」は「 $x-t$ グラフの傾き」に相当する。

　さらに、点 $\text{C}$ での瞬間の速度を求めるには時間 $\Delta t$ を小さくしていけばよい。即ち $\Delta t \to 0$ の極限を考えればよく

$\begin{eqnarray*} \text{瞬間の速度}\ v =\lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t} =\lim_{\Delta t \to 0} \frac{x(t+\Delta t) - x(t)}{\Delta t} =\frac{\diff x}{\diff t} \end{eqnarray*}$

となる。「瞬間の速度」は通常、単に「速度」と表現する。

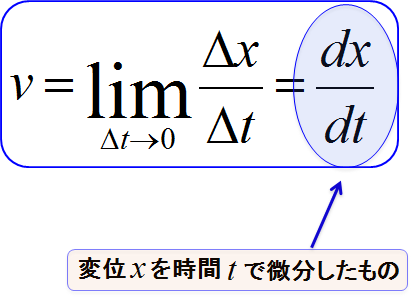
　ここで、「微分」が登場した。数学の学習がまだの状態では理解は難しいかもしれない。
では、何故「微分」が必要になったかと言えば、極限を考えたからである。「曲線の傾き」を求めるには「微分」を導入せざるを得ない。しかし、「平均」であれば極限は考えなくても良いし、 $x-t$ グラフが「曲線」でなく「直線」であれば「微分」は必要ないことになる。

　物理と数学は密接に関係していることを知っておこう。かの「ニュートン」さんは力学を理解するために微積分学の体系に力を入れたほどである。
　高校物理では原則として「微積は使用しない」という指導要領があるので、多少仕方がない部分もあるが、残念なことである。大学の物理で数学をガンガン使用することに戸惑う学生が居るのはこのあたりに原因があるかもしれない。

加速度

　加速度の定義を理解するには $v-t$ グラフは欠かせない。加速度は「時間に対する速度の変化率」である。
　下図のような $v-t$ グラフを考え、点 $\text{P}$ から点 $\text{P'}$ までの移動中のある点 $\text{C}$ を考える。

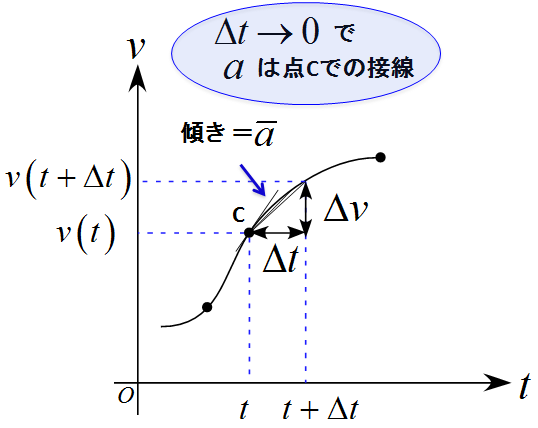
ここで点 $\text{C}$ を通過する時刻 $t$ から時間 $\Delta t$ 後までの速度変化 $\Delta v$ は

$\begin{eqnarray*} \Delta v = v(t+\Delta t) - v(t) \end{eqnarray*}$

と表される。

　従って、「時間 $\Delta t$ に対する速度変化 $\Delta v$ の変化率」は

$\begin{eqnarray*} \text{変化率} = \frac{\Delta v}{\Delta t} = \frac{v(t+\Delta t) - v(t)}{\Delta t} \end{eqnarray*}$

である。これを「平均の加速度 $\bar{a}$ 」と呼ぶ。

この「変化率」は「 $v-t$ グラフの傾き」に相当する。

さらに、点 $\text{C}$ での瞬間の加速度を求めるには時間 $\Delta t$ を小さくしていけばよい。即ち $\Delta t \to 0$ の極限を考えればよく

$\begin{eqnarray*} \text{瞬間の加速度}\ a =\lim_{\Delta t \to 0} \frac{\Delta v}{\Delta t} =\lim_{\Delta t \to 0} \frac{v(t+\Delta t) - v(t)}{\Delta t} =\frac{\diff v}{\diff t} \end{eqnarray*}$

となる。「瞬間の加速度」は通常、単に「加速度」と表現する。

さらに、前出の速度の定義を合わせると

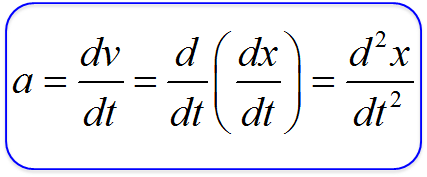
となる。

　ここでも、加速度を「微分」使って表したが、「平均」を考える場合や「 $v-t$ グラフが直線」の場合には極限の考えを導入する必要がない。

変位～速度～加速度の関係

　さらに、この速度・加速度の定義からそれぞれの関係についてまとめると下図のようになる。

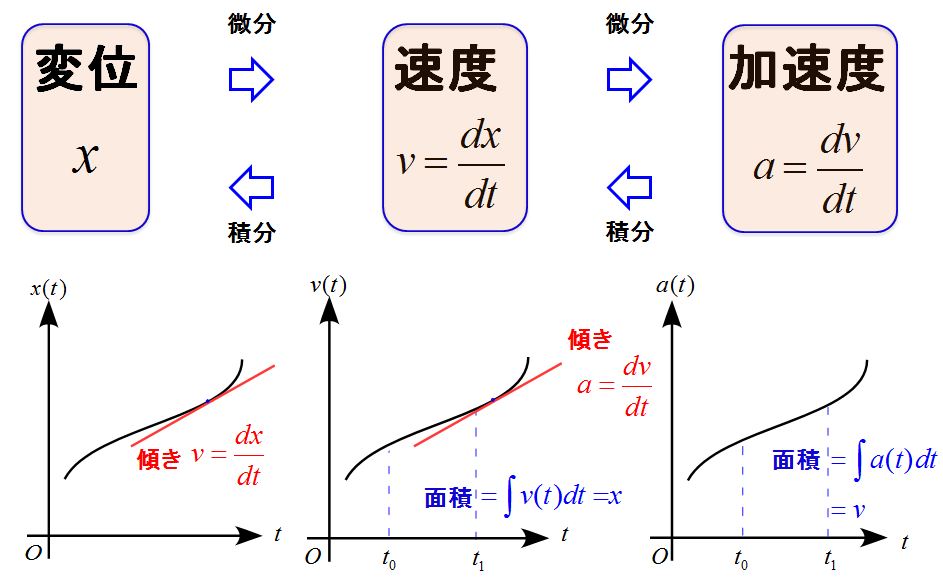
変位 $x$ を時間 $t$ で微分すれば速度 $v$ になる。
速度 $v$ を時間 $t$ で積分すれば変位 $x$ になる。
速度 $v$ を時間 $t$ で微分すれば加速度 $a$ になる。
加速度 $a$ を時間 $t$ で積分すれば速度 $v$ になる。

これらの関係は $x-t$ グラフや $v-t$ グラフを考えれば導かれるものである。