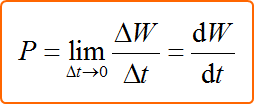仕事率の定義
機械などに仕事をさせる場合、仕事の量だけでなく「どれだけ速く作業するか」が問題となってくる。このような効率を考える場合「単位時間あたりの仕事量」で表し、これを「仕事率$P$」と呼ぶ
\begin{eqnarray*}
P = \lim_{\Delta t \to 0} \frac{\Delta W}{\Delta t} =\frac{\diff W}{\diff t}
\end{eqnarray*}
- 仕事率は英語の「power」の頭文字で表すことが多い。
仕事率の次元
仕事率の次元は、定義$P=\displaystyle \frac{\diff W}{\diff t}$より
\begin{eqnarray*}
\text{仕事率の次元} = \frac{\frac{[ML^2]}{[T^2]}}{[T]} =\frac{[ML^2]}{[T^3]}
\end{eqnarray*}
と表される。
$\text{MKS}$単位系で単位を表すと
\begin{eqnarray*}
\text{仕事率の単位} = [\mbox{W}] = [\mbox{J/s}] = [ (\mbox{kg m}^2 \mbox{/s}^2 ) /\mbox{s} ] = [ \mbox{kg m}^2 \mbox{/s}^3 ]
\end{eqnarray*}
となる。
- 仕事率の単位$[\mbox{W}]$は「ワット (watt)」と表す。
- $1 \ [\mbox{W}]= 1 [\mbox{J/s}]$である。
仕事率と速度
仕事率の定義$P=\displaystyle \frac{\diff W}{\diff t}$は仕事の定義$W = \vec{F}\cdot \vec{r}$より
\begin{eqnarray*}
P &=& \frac{\diff W}{\diff t} \\
\\
&=& \frac{\vec{F}\cdot \diff \vec{r}}{\diff t} \\
\\
&=& \vec{F} \cdot \frac{\diff \vec{r}}{\diff t} \\
\\
&=& \vec{F} \cdot \vec{v}
\end{eqnarray*}
と変形でき、仕事率$P$は力$F$と速度$v$の内積でも表されることがわかる。
まとめ
「仕事率$P$」は「単位時間あたりの仕事量」で表す。