力学 ~ 物体に作用する力と作図で運動方程式を立てる方法 part-1

　力学は運動方程式が重要であり、運動方程式ができてしまえば7~8割が終わったようなものである。しかし、運動方程式を正しく立てられず、現象が理解できない学生も見受けられる。正しく運動方程式が立てられないケースの内、多くが正しく作図(イメージ図)が描けていないようである。
　そこで、ここではよくある物理モデルのイメージ図を描き、作用する力を書き込み、運動方程式を立てるまでを解説する。

イメージ図について

• 多くの場合、物体は「質点」と考えて計算している。(質量を持った点)
  従って、○とか□の図はあくまでイメージである。(点では判りにくい)
• 質点なので力の矢印の始点はあまり重要ではない。
• 矢印を書き込む物体は運動の途中の図が良い。

軸の設定について

• 軸の向きは基本的に自由に設定して良い。
• 問題文で指定されている場合はそれを利用する。
• 指定が無い場合は自分で都合の良い方向を正とする。
• 一般的には運動の進行方向を正に設定すると良いことが多い。
• 直線的な運動は1つ、平面的は2つ、立体的は3つの軸を設定する。
• 運動の種類によっては極座標を用いて表す場合がある。

物体に作用する力の探し方

物体に作用する力の探す手順は以下の順に行う。

1. 場の力

　まずは場の力の有無を確認する。多くの場合は重力場を想定しているので「重力$mg$」が作用する力となる。問題の設定によっては「電場」や「磁場」を考える必要がある。
重力$mg$の源は万有引力である。従って力は地球の中心方向に向くので作図をする場合は真下に矢印を書き込むことになる。

2. 接触力

　文字通り、接触するものから受ける力を指す。描いたイメージ図の物体のまわりを見て書き込む。接触面からの抗力、糸の張力、バネの復元力等がある。

3. 慣性力

　設定した軸自体が動いている場合には慣性力が生じる。具体例としてはエレベータ内を運動する物体、電車内を運動する物体等がある。このようなモデルでは軸を乗り物内に設定する場合が多く、軸自体が動くことになるので軸の動く方向(乗り物の動く方向)の逆向きに$m\alpha$の力を受ける。(乗り物の加速度は$\alpha$とした)

運動方程式について

• まず、何も考えず左辺に$ma$と書く。
  軸が複数ある場合は添字を付けて$ma_x,\ ma_y$等とする。
• 軸の向きに注意しながら物体に作用する力を書く。
• 軸の向きは加速度$a$の正の向きと一致する。
• 運動方程式は軸ごとに立てる。
  直線運動は1つ、平面運動は2つ、立体運動は3つの運動方程式ができる。
• 物体が静止、またはつり合っている状態でも運動方程式を書く。運動方程式は$a=0$の場合も含めて成立する。(余計な場合分けをする必要はない。運動方程式を立てた後、$a=0$とすれば良い)
• 問題文の設定に合わせて式を書き変える。

自由落下

自由落下のモデル図

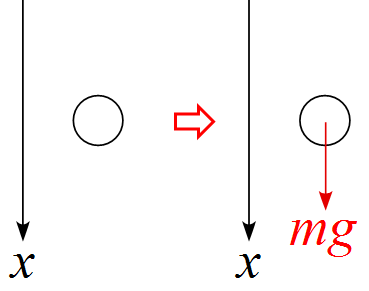
・軸の向きは上下どちらでも良い。問題の設定に合わせれば良い。
・作用する力は重力$mg$のみである。
・作用する点は重心とし、矢印の始点とした。

自由落下の運動方程式

運動方程式は

\begin{eqnarray*}
ma &=&mg \\
\\
m\frac{\diff v}{\diff t} &=& mg
\end{eqnarray*}

となる。

・上図の例のように下向きを正として設定した運動方程式となる。従って、重力$mg$は軸の向きと一致するので正となる。
・もし、軸を上向きを正に設定したのであれば$ma=-mg$となる。

速度に比例した空気抵抗がある物体の落下

速度に比例した空気抵抗がある物体の落下のモデル図

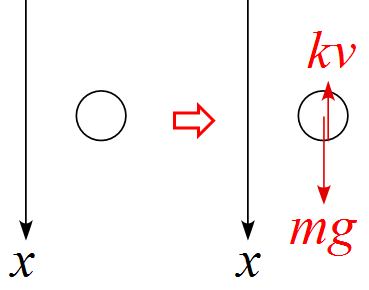
・軸の向きは上下どちらでも良い。問題の設定に合わせれば良い。例では進行方向である下向きを正とした。
・作用する力は重力$mg$と速度に比例した空気抵抗による力$kv$である。比例定数$k(>0)$とした。
・抵抗力$kv$は下の面に抵抗がありそうなイメージなので物体の下を矢印の始点にして描いたが、重心を始点としても良い。そもそも物体は質点として計算するので矢印の始点の位置は大して重要ではない。

速度に比例した空気抵抗がある物体の落下の運動方程式

運動方程式は

\begin{eqnarray*}
ma &=& mg-kv \\
\\
m\frac{\diff v}{dt} &=& mg-kv
\end{eqnarray*}

となる。

・下向きを正と設定した運動方程式である。
・この微分方程式を解くのは一手間が必要である。(単に$t$の次数が上がる訳ではない)
・この運動方程式を解くと

\begin{eqnarray*}
v(t) = \frac{mg}{k} \left( 1- e^{-\frac{k}{m} t} \right)
\end{eqnarray*}

となる。

鉛直投げ上げ (初速度$v_0$)

鉛直投げ上げのモデル図

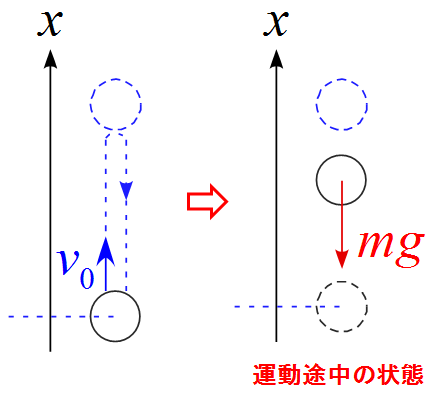
・とりあえず、軸の向きは上を正に設定した。
・作用する力は重力$mg$のみである。
・初速度$v_0$は物体に作用する力とは関係ない。

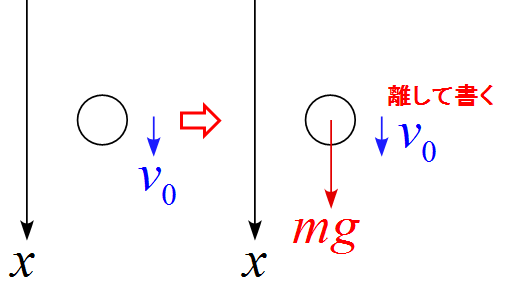
ダメなイメージ図

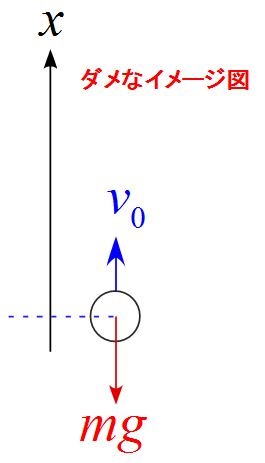
と描くと間違える元なので注意をする。

・作図は運動の途中の状態で描くと良い。

鉛直投げ上げの運動方程式

運動方程式は
\begin{eqnarray*}
ma &=& -mg \\
\\
m\frac{\diff v}{\diff t} &=& -mg
\end{eqnarray*}
となる。

・上向きを正に設定したので重力$mg$は逆向きとなりマイナスである。
・運動方程式自体は上向きを正に設定した自由落下と同じになる。
・初期条件である初速度$v_0$は運動方程式を解くと出てくる積分定数を決めるもの。

鉛直投げ下ろし (初速度$v_0$)

鉛直投げ下ろしのモデル図

・とりあえず、軸の向きは下向きを正に設定した。
・作用する力は重力$mg$のみである。

鉛直投げ下ろしの運動方程式

運動方程式は
\begin{eqnarray*}
ma &=& mg \\
\\
m\frac{\diff v}{\diff t} &=& mg
\end{eqnarray*}
となる。

・運動方程式自体は下向きを正と設定した自由落下と同じである。

水平投射 (初速度$v_0$)

水平投射のモデル図

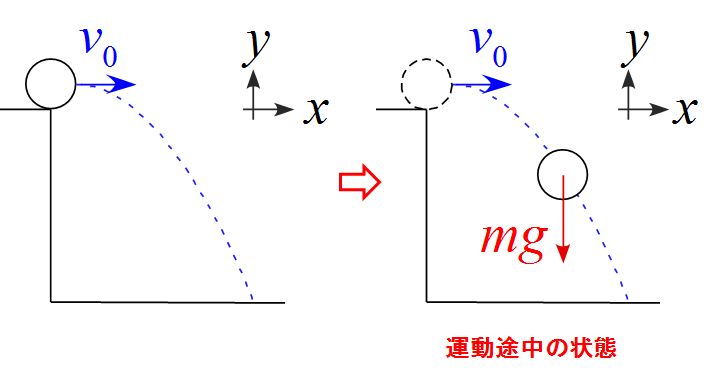
・平面的に運動するので軸は2つ設定する。
・$x$軸は右向きを正、$y$軸は上向きを正とした。
・作用する力は重力$mg$のみである。
・初速度$v_0$は力とは無関係である。

水平投射の運動方程式

運動方程式は
\begin{eqnarray*}
ma_x &=& 0 \\
\\
ma_y &=& -mg \\
\\
\\
m\frac{\diff v_x}{\diff t} &=& 0
\\
\\
m\frac{\diff v_y}{\diff t} &=& -mg
\end{eqnarray*}
となる。

・$x$軸方向には作用する力は無いので右辺はゼロになる。
・$y$軸方向に作用する力は重力$mg$のみであり、上向きを正に設定しているので$-mg$となる。
・$x$軸方向の運動は作用する力が無いので等速度運動(等速直線運動)である。
・$y$軸方向の運動は上向きを正とした自由落下と同じになる。

斜方投射

斜方投射のモデル図

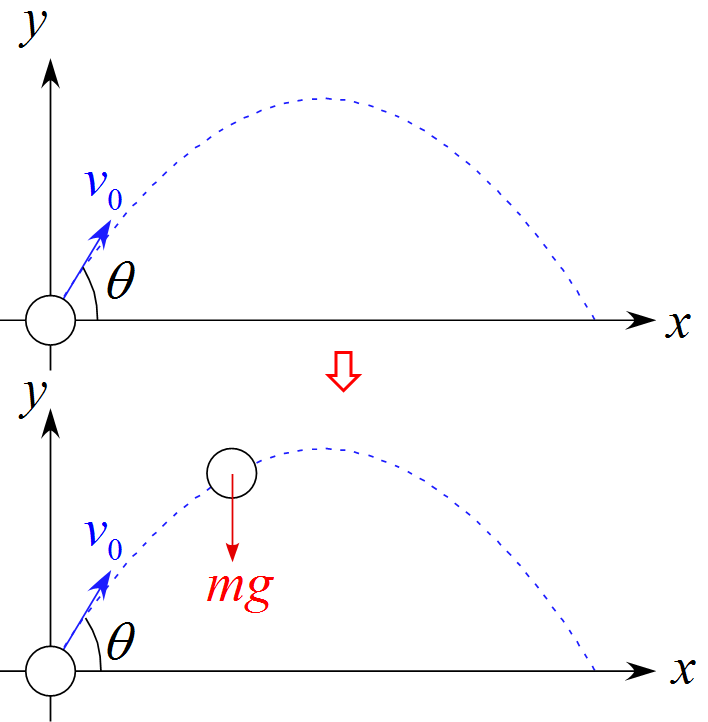
・平面的に運動するので軸は2つ設定する。
・$x$軸は右向きを正、$y$軸は上向きを正とした。
・作用する力は重力$mg$のみである。
・初速度$v_0$は力とは無関係である。
・初速度である初速度$v_0$は次の図のように分解できる。

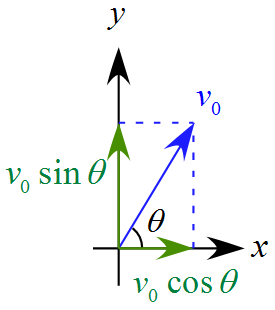
斜方投射の運動方程式

運動方程式は
\begin{eqnarray*}
ma_x &=& 0 \\
\\
ma_y &=& -mg \\
\\
\\
m\frac{\diff v_x}{\diff t} &=& 0
\\
\\
m\frac{\diff v_y}{\diff t} &=& -mg
\end{eqnarray*}
となる。
(初速度$v_0$)

・$x$軸方向には作用する力は無いので右辺はゼロになる。
・$y$軸方向に作用する力は重力$mg$のみであり、上向きを正に設定しているので$-mg$となる。
・$x$軸方向の運動は作用する力が無いので等速度運動(等速直線運動)である。
・$y$軸方向の運動は上向きを正とした自由落下と同じになる。
・運動方程式自体は水平投射と同様で、初期条件の違いが運動の違いである。

天井から糸でつるされた物体

天井から糸でつるされた物体のモデル図

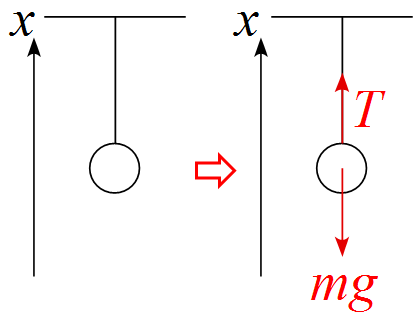
・軸は上向きを正と設定した。
・作用する力は重力$mg$と接触力である張力$T$ (tenson) である。

天井から糸でつるされた物体の運動方程式

運動方程式は
\begin{eqnarray*}
ma= T-mg
\end{eqnarray*}
と記述できる。

ここで、物体が静止しているのであれば束縛条件より$a=0$となり

運動方程式は
\begin{eqnarray*}
0= T-mg
\end{eqnarray*}
となり、所謂、つり合い式となる。

・運動方程式は$a=0$(静止 or つり合い)の場合も含んで成立するので、原則として運動方程式を立ててから$a=0$として条件を絞り込む。

天井からばねでつるされた物体 (ばね定数は$k$)

天井からばねでつるされた物体のモデル図

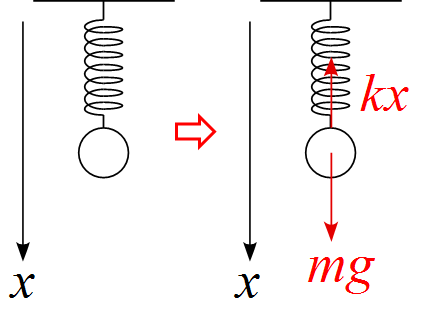
・軸はばねが伸びる方向である下向きを正と設定した。
・作用する力は重力$mg$と接触力であるばねの復元力$kx$である。

天井からばねでつるされた物体の運動方程式

運動方程式は
\begin{eqnarray*}
ma &=& mg-kx \\
\\
m\frac{\diff ^2 x}{\diff t^2} &=& mg-kx
\end{eqnarray*}
となる。

・この微分方程式を解くのは一手間が必要である。(単に$t$の次数が上がる訳ではない)
・この運動方程式の一般解は

\begin{eqnarray*}
x(t) = Asin (\omega t + \phi)
\end{eqnarray*}

となる。但し、$\omega^2 = \frac{m}{k} ,\ A\text{は振幅},\ \phi\text{は初期位相} $である。