力のモーメント ~ 練習問題 part-4
力のモーメントに関連した練習問題を取り上げる。
天井から水平につられた棒
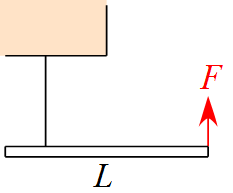
図のように、長さ$L$,質量$m$の棒の1点に糸を取り付け、棒の右端に力$F$を鉛直上向きに作用させたところ棒は水平状態を保った。
このときの糸の張力$T$を求めよ。また、糸が取り付けられた位置は棒の左端からどれだけか答えよ。
解答
作用する力を書き込む
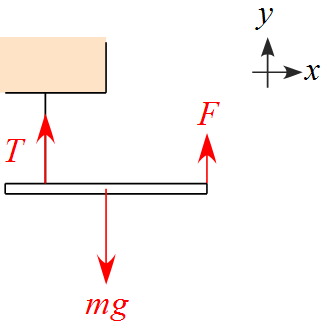
- 作用する力は棒の質量による重力$mg$、作用させた力$F$、糸の張力$T$の3つである。
- 重力$mg$は棒の重心に作用しているとする。
運動方程式を立てる
運動方程式は$y$軸方向のみ立てると
\begin{eqnarray*}
m a_y &=& T+F -mg
\end{eqnarray*}
と記述できる。
束縛条件$a_y =0$より
\begin{eqnarray*}
0 &=& T+F -mg\\
\\
T &=& mg -F
\end{eqnarray*}
となる。
位置ベクトル$\vec{r}_1 ,\ \vec{r}_2$を設定
糸を取り付けた点を原点$O$とし、下図の様に位置ベクトル$\vec{r}_1 ,\ \vec{r}_2$を設定する。
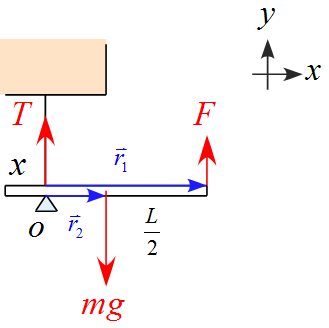
位置ベクトル$\vec{r}_1 ,\ \vec{r}_2$は
\begin{eqnarray*}
\vec{r}_1 &=&
\begin{pmatrix}
L-x \\
0 \\
0 \\
\end{pmatrix} ,\ \quad
\vec{r}_2 &=&
\begin{pmatrix}
\frac{L}{2}-x \\
0 \\
0 \\
\end{pmatrix} \\
\end{eqnarray*}
である。
作用する力をベクトルとして表す
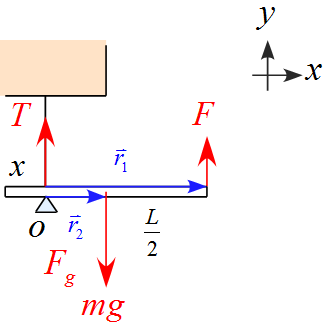
重力は$\vec{F}_g$と添え字を設定する。今回は糸を取り付けた地点を支点として計算するので張力$T$は力のモーメントを生じないので、$\vec{F}$と$\vec{F}_g$を書き出すと
棒に作用する力$\vec{F} ,\ \vec{F}_g $は
\begin{eqnarray*}
\vec{F} &=&
\begin{pmatrix}
0 \\
F \\
0 \\
\end{pmatrix} ,\ \quad
\vec{F}_g &=&
\begin{pmatrix}
0 \\
-mg \\
0 \\
\end{pmatrix}
\end{eqnarray*}
である。
力のモーメントを計算する
教科書的計算
力のモーメント$\vec{M}$の大きさは
\begin{eqnarray*}
| \vec{M} | = |\vec{r}||\vec{F}| \sin \theta
\end{eqnarray*}
より
\begin{eqnarray*}
| \vec{M}_1 | &=& |\vec{r}_1||\vec{F}| \sin \theta \\
\\
&=& (L-x) \cdot F \sin 90^{\circ} \\
\\
&=& (L-x)F
\end{eqnarray*}
\begin{eqnarray*}
| \vec{M}_2 | &=& |\vec{r}_2||\vec{F}_g| \sin \theta \\
\\
&=& \left( \frac{L}{2}-x \right) \cdot mg \sin (-90^{\circ}) \\
\\
&=& - \left( \frac{L}{2}-x \right) mg
\end{eqnarray*}
であるから
水平状態をを保つためには
\begin{eqnarray*}
M = M_1 +M_2 = (L-x)F + \left[ - \left( \frac{L}{2}-x \right) mg \right] =0
\end{eqnarray*}
となる。
式を整理すると
\begin{eqnarray*}
(L-x)F + \left[ - \left( \frac{L}{2}-x \right) mg \right] &=& 0 \\
\\
LF - xF - \frac{Lmg}{2} + xmg &=& 0 \\
\\
x(mg-F) &=& \frac{Lmg}{2} -LF \\
\\
x(mg-F) &=& \left (\frac{mg}{2} -F \right) L \\
\\
x&=& \frac{\left (\frac{mg}{2} -F \right) L}{mg-F} \\
\\
x&=& \frac{mg-2F}{2(mg-F)} L
\end{eqnarray*}
となる。