仕事の原理
「たとえ、どんなに便利な道具を用いて物体を動かすのに必要な力を小さくしても、決して仕事で得をすることは無い」
仕事の原理の具体例 ~ 滑車を用いる
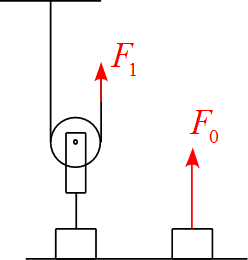
軸を設定し、作用する力を書き込む
- 上向きに$x$軸の正を設定する。
- 単に引き上げる場合、作用する力は重力$mg$と引き上げる力$F_0$の2つである。
- 滑車を用いる場合、作用する力は重力$mg$と引き上げる力$F_1$と天井に接続されている糸の張力$T$の和である。
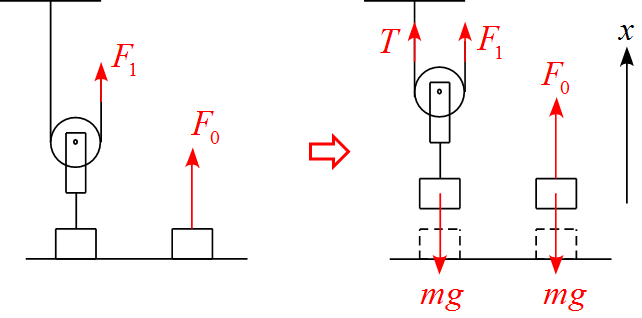
運動方程式を立てる ~ 単に引き上げる場合
運動方程式は
\begin{eqnarray*}
ma = F_0 - mg
\end{eqnarray*}
となる。
仕事を計算する ~ 単に引き上げる場合
仕事は
\begin{eqnarray*}
m \frac{\diff v}{\diff t} &=& F_0 - mg \\
\\
\int m \frac{\diff v}{\diff t} \diff x &=& \int ( F_0 - mg ) \diff x \\
\\
\int m \frac{\diff v}{\diff t} v \diff t &=& \int ( F_0 - mg ) \diff x \\
\\
\int \frac{\diff }{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t &=& \int ( F_0 - mg ) \diff x \\
\end{eqnarray*}
となる。
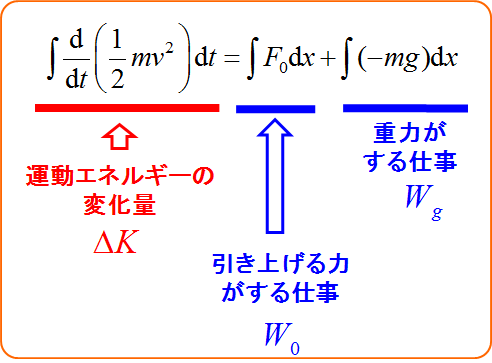
ゆっくり引き上げる(準静的)ので左辺は$0$になる。
よって
\begin{eqnarray*}
0 &=& \int F_0 \diff x + \int ( - mg ) \diff x \\
\\
0 &=& W_0 + W_g \\
\end{eqnarray*}
となる。
物体を$h$だけ引き上げるとすると
\begin{eqnarray*}
W_0 &=& - W_g \\
\\
&=& \int_{0}^{h} mg \diff x \\
\\
&=& [mgx]_0^h \\
\\
&=& mgh
\end{eqnarray*}
となる。
運動方程式を立てる ~ 滑車を用いる場合
運動方程式は
\begin{eqnarray*}
ma = F_0 +T - mg
\end{eqnarray*}
となる。
仕事を計算する ~ 単に引き上げる場合
仕事は
\begin{eqnarray*}
m \frac{\diff v}{\diff t} &=& F_0 + T - mg \\
\\
\int m \frac{\diff v}{\diff t} \diff x &=& \int ( F_0 +T - mg ) \diff x \\
\\
\int m \frac{\diff v}{\diff t} v \diff t &=& \int ( F_0 + T - mg ) \diff x \\
\\
\int \frac{\diff }{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t &=& \int ( F_0 + T - mg ) \diff x \\
\end{eqnarray*}
となる。
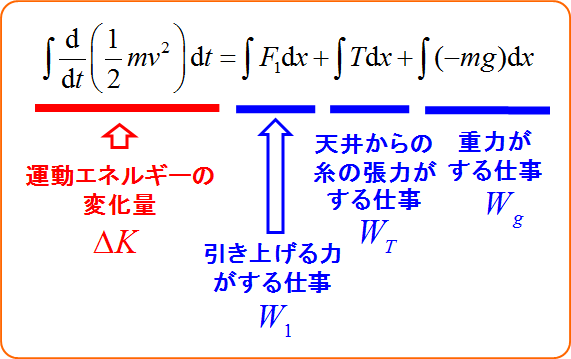
ゆっくり引き上げる(準静的)ので左辺は$0$になる。
よって
\begin{eqnarray*}
0 &=& \int F_1 \diff x + \int T \diff x + \int ( - mg ) \diff x \\
\end{eqnarray*}
となる。
ここで、糸はたるまないので$T=F_1$となるので
\begin{eqnarray*}
0 &=& \int F_1 \diff x + \int F_1 \diff x + \int ( - mg ) \diff x \\
\\
0 &=& 2 \int F_1 \diff x + \int ( - mg ) \diff x \\
\\
0 &=& 2 W_1 + W_g \\
\\
\end{eqnarray*}
物体を$h$だけ引き上げるとすると、引き上げる距離は$2h$必要となるので
\begin{eqnarray*}
W_1 &=& -\frac{1}{2} W_g \\
\\
&=& \frac{1}{2} \int_{0}^{2h} mg \diff x \\
\\
&=& \frac{1}{2}[mgx]_0^{2h} \\
\\
&=& \frac{1}{2}mg \cdot 2h \\
\\
&=& mgh
\end{eqnarray*}
となり、直接引き上げた場合と同じ結果となる。
仕事の原理の具体例 ~ 滑らかな斜面を引き上げる
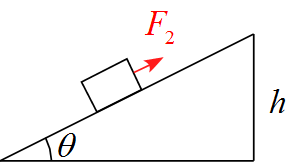
軸を設定し、作用する力を書き込む
- 斜面に沿って上向きを$x$軸の正に、斜面に垂直な方向上向きを$y$軸の正に設定する。
- 作用する力は重力$mg,\ $面からの抗力$N(R), \ $引き上げる力$F_2$の3つである。
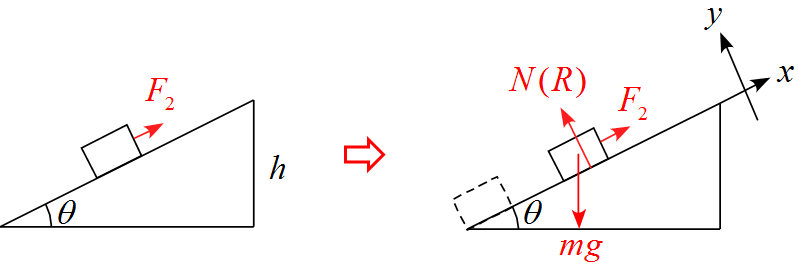
斜面に沿った成分に分解すると
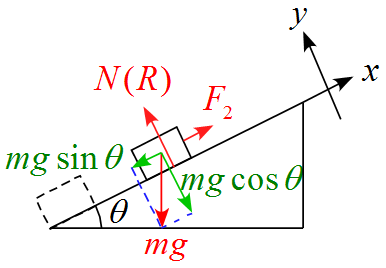
となる。
運動方程式を立てる ~ 滑車を用いる場合
運動方程式は
\begin{eqnarray*}
m a_x &=& F_2 - mg \sin \theta \\
\\
m a_y &=& N - mg \cos \theta \\
\end{eqnarray*}
となる。
仕事を計算する ~ 滑車を用いる場合
$x$方向の運動方程式に対して$x$積分すると
運動方程式は
\begin{eqnarray*}
m a_x &=& F_2 - mg \sin \theta \\
\\
m \frac{\diff v_x}{\diff t} &=& F_2 - mg \sin \theta \\
\\
\int m \frac{\diff v_x}{\diff t} \diff x &=& \int ( F_2 - mg \sin \theta ) \diff x \\
\\
\int m \frac{\diff v_x}{\diff t} v_x \diff t &=& \int ( F_2 - mg \sin \theta ) \diff x \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2} mv_x^2 \right) \diff t &=& \int ( F_2 - mg \sin \theta ) \diff x \\
\end{eqnarray*}
となる。
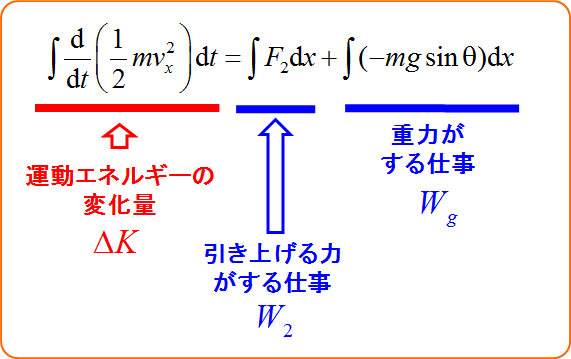
ゆっくり引き上げる(準静的)ので左辺は$0$になる。
よって
\begin{eqnarray*}
0 &=& \int F_2 \diff x + \int ( - mg \sin \theta ) \diff x \\
\\
0 &=& W_2 + W_g
\end{eqnarray*}
となる。
斜面を引き上げる距離$L$は下図より
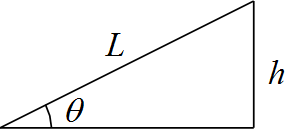
\begin{eqnarray*}
\sin \theta &=& \frac{h}{L} \\
\\
L &=& \frac{h}{\sin \theta}
\end{eqnarray*}
である。
従って、仕事は
\begin{eqnarray*}
W_2 &=& - W_g \\
\\
&=& \int_{0}^{L} mg \sin \theta \diff x \\
\\
&=& [(mg \sin \theta) x ]_0^{L} \\
\\
&=& mgL \sin \theta \\
\\
&=& mg \frac{h}{\sin \theta} \sin \theta \\
\\
&=& mgh
\end{eqnarray*}
となり、直接引き上げた場合と同じ結果となる。