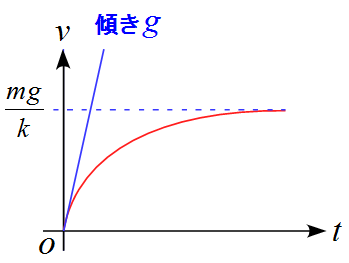
雨滴の落下 ~ 空気抵抗が働く運動
雨滴の落下の運動を考える。空から雨が降ってくるモデルにおいて、もし空気抵抗が無いとする。この時、例えば上空$1 \ \mbox{km}$ から落下したとすると
\begin{eqnarray*}
v(t) &=& \sqrt{ 2gx} \\
\\
&=& \sqrt{2\times 9.8 \ \mbox{m/s}^2 \times 1000 \ \mbox{m} } \\
\\
&=& 140 \ \mbox{m/s}
\end{eqnarray*}
と計算できる。
結構な速さで、当たると大怪我をしてしまいそうである。しかし、我々は雨が降って大怪我をしたことは無い。これは、空気による抵抗があり速度が抑えられているからである。空気抵抗の扱いについては複数のモデルが考えられるが、ここでは速度に比例した空気抵抗$kv$が作用したとして考えてみよう。
運動方程式を立てる
「力学 ~ 物体に作用する力と作図で運動方程式を立てる方法 part-1 速度に比例した空気抵抗がある物体の落下」でも取り上げた様に、
まずは軸を設定し、作用する力を書き出すと
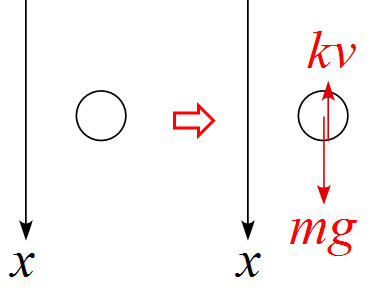
従って、運動方程式は
\begin{eqnarray*}
ma &=& mg - kv \\
\\
m\frac{\diff v}{\diff t} &=& mg-kv
\end{eqnarray*}
と表すことができる。
左辺と右辺の第2項に$v$を含んでいる微分方程式である。
運動方程式が示す意味を検討する
この微分方程式を解くのは別の機会として、この式が何を表しているか大雑把に検討する。
運動方程式を式変形すると
\begin{eqnarray*}
\frac{\diff v}{\diff t} &=& g- \frac{k}{m}v
\end{eqnarray*}
$v$が小さい所では$- \frac{k}{m} v \simeq 0$と考えると
\begin{eqnarray*}
\frac{\diff v}{\diff t} \simeq g
\end{eqnarray*}
となるので、$v-t$グラフの傾きが$g$である。
$a=0$となる時、等速直線運動であり、重力$mg$と空気抵抗$kv$がつり合うときとなる。
\begin{eqnarray*}
0 &=& g- \frac{k}{m}v \\
\\
v &=& \frac{mg}{k}
\end{eqnarray*}
となる。
運動方程式を解いた結果を用いてグラフを検討する
この運動の運動方程式を解くと
\begin{eqnarray*}
v (t) &=& \frac{mg}{k} \left( 1- e^{-\frac{k}{m}t} \right)
\end{eqnarray*}
となる。
加速度$a$について
\begin{eqnarray*}
a = \frac{\diff v}{\diff t} &=& \frac{\diff}{\diff t} \left[ \frac{mg}{k} \left( 1- e^{-\frac{k}{m}t} \right) \right] \\
\\
&=& \frac{mg}{k} \left( -e^{-\frac{k}{m}t} \right) \cdot -\frac{k}{m} \\
\\
&=& g e^{-\frac{k}{m}t}
\end{eqnarray*}
よって、
\begin{eqnarray*}
a (0) &=& g e^{-\frac{k}{m}\cdot 0} = g \\
\\
a (\infty) &=& e^{-\frac{k}{m}\cdot \infty} 0
\end{eqnarray*}
となり、$v-t$グラフのスタートは傾き$g$で十分に時間が経つと傾きが$0$になる。つまり、ある一定値に漸近することがわかる。
速度$v$について
\begin{eqnarray*}
v (0) &=& \frac{mg}{k} \left( 1- e^{-\frac{k}{m}\cdot 0 } \right) = \frac{mg}{k} \left( 1- e^{0} \right) =0 \\
\\
v (\infty) &=& \frac{mg}{k} \left( 1- e^{-\frac{k}{m}\cdot \infty } \right) = \frac{mg}{k} \left( 1- e^{-\infty} \right) =\frac{mg}{k}
\end{eqnarray*}
となり、$v-t$グラフの原点を通り、十分に時間が経つと一定値$\frac{mg}{k}$に漸近する。この一定値を「終端速度 (terminal velocity)」と呼ぶ。