仕事とエネルギー ~ 練習問題 part-7

仕事とエネルギー ~ 練習問題 part-7

縮めたバネの仕事

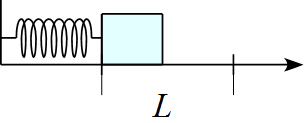
　下図のようにバネの一端が壁に固定され、他端は自由な状態である。このバネに質量$m$の物体を押し付けバネを$L$だけ縮めて放したところバネが自然長になった位置で物体とバネが離れた。
以下の問に答えよ。但し、バネ定数は$k$とする。

(1) 水平面が滑らかなで摩擦がない場合、この運動での仕事とエネルギーについて検討せよ。

(2) 水平面が荒く摩擦が作用する場合、この運動での仕事とエネルギーについて検討せよ。

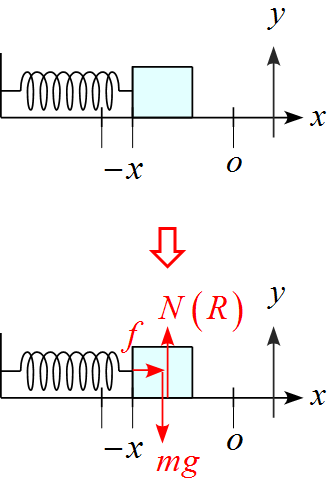
解答 ~ 水平面が滑らかなで摩擦がない場合

軸を設定し、作用する力を書き込む

• $x$軸の正の向きは右側に、$y$軸の正の向きは上に設定した。
• バネの自然長の位置を原点とした。
• 作用する力は重力$mg , \ $面からの抗力$N(R) ,\ $バネが物体を押す力$f$の3つである。

運動方程式を立てる

　運動方程式は
\begin{eqnarray*}
m a_x &=& f \\
\\
m a_y &=& N - mg
\end{eqnarray*}
となる。

となる。
束縛条件より$a_y=0$であるから

\begin{eqnarray*}
ma_x &=& f \\
\\
0 &=& N - mg
\end{eqnarray*}
となる。
ここで、バネの復元力の大きさ$F$はバネ定数$k$とするとフックの法則$F =kx$となる。
従って、位置が$ｰx$のバネが物体を押す力$f$は
\begin{eqnarray*}
f = k (-x) = -kx
\end{eqnarray*}
となる。

仕事を計算する ~ 両辺を$x$で積分する

　$x$軸の運動に着目するので$a_x = a$と書き換えて両辺を$x$で積分すると

\begin{eqnarray*}
ma &=& - kx \\
\\
m \frac{\diff v}{\diff t} &=& - kx \\
\\
\int m \frac{\diff v}{\diff t} \diff x &=& \int ( - kx) \diff x \\
\\
\int m \frac{\diff v}{\diff t} v \diff t &=& \int ( - kx) \diff x \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t &=& \int (- kx) \diff x
\end{eqnarray*}
となる。

　ここで物体から手を放したした時刻を$t=0$とし、初期条件を$v(0) = v_0 =0 ,\ v(t) = v ,\ x(0) = -L ,\ x(t) = x$とすると

\begin{eqnarray*}
\int \frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t &=& \int (- kx) \diff x \\
\\
\left[ \frac{1}{2} mv^2(t) \right]_{0}^{t} &=& \left[-\frac{1}{2}k x^2 \right]_{-L}^{x} \\
\\
\frac{1}{2} mv^2(t) - \frac{1}{2} mv^2(0) &=& -\frac{1}{2}k x^2 - \left[-\frac{1}{2}k (-L)^2\right] \\
\\
\frac{1}{2} mv^2 - \frac{1}{2}m \cdot 0^2 &=&-\frac{1}{2}k x^2 - \left(-\frac{1}{2}k L^2\right) \\
\\
\frac{1}{2} mv^2 +\frac{1}{2}k x^2 &=&\frac{1}{2}k L^2
\end{eqnarray*}
となる。
この式が所謂、エネルギー保存則を表した式である。

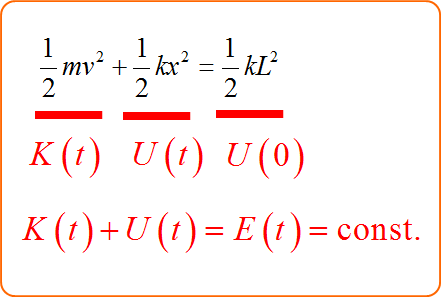
　時刻を$t_1$でバネと物体が離れたとすると、離れた瞬間の速度$v_1$は

\begin{eqnarray*}
\frac{1}{2} mv_1^2 +\frac{1}{2}k \cdot 0^2 &=&\frac{1}{2}k L^2 \\
\\
v_1^2 &=& \frac{k}{m}L^2 \\
\\
v_1 &=& \sqrt{\frac{k}{m}} L
\end{eqnarray*}
となる。

解答 ~ 水平面が荒く摩擦が作用する場合

軸を設定し、作用する力を書き込む

• $x$軸の正の向きは右側に、$y$軸の正の向きは上に設定した。
• バネの自然長の位置を原点とした。
• 作用する力は重力$mg , \ $面からの抗力$R ,\ $バネが物体を押す力$f$の3つである。

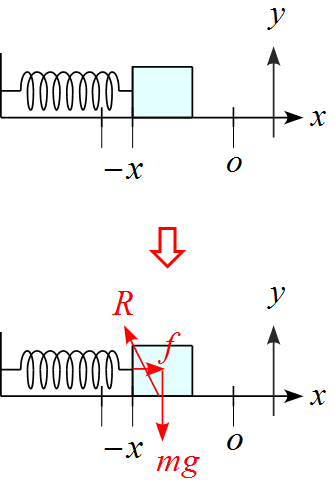
$x,y$軸に沿った成分に分解すると

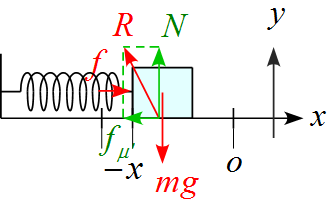
• 分解した成分の矢印が重なるので、矢印の始点をずらして表した。

運動方程式を立てる

　運動方程式は
\begin{eqnarray*}
m a_x &=& f - f_{\mu'}\\
\\
m a_y &=& N - mg
\end{eqnarray*}
となる。

となる。
束縛条件より$a_y=0$であるから

\begin{eqnarray*}
ma_x &=& f - f_{\mu'} \\
\\
0 &=& N - mg
\end{eqnarray*}
となる。
ここで、バネの復元力の大きさ$F$はバネ定数$k$とするとフックの法則$F =kx$となる。
従って、位置が$ｰx$のバネが物体を押す力$f$は
\begin{eqnarray*}
f = k (-x) = -kx
\end{eqnarray*}
となる。
また、動摩擦係数の定義$\mu' = \displaystyle \frac{f_{\mu'}}{N}$より
\begin{eqnarray*}
f_{\mu'} &=& \mu' N \\
&=& \mu' mg
\end{eqnarray*}
となる。

仕事を計算する ~ 両辺を$x$で積分する

　$x$軸の運動に着目するので$a_x = a$と書き換えて両辺を$x$で積分すると

\begin{eqnarray*}
ma &=& - kx -\mu' mg\\
\\
m \frac{\diff v}{\diff t} &=& - kx -\mu' mg \\
\\
\int m \frac{\diff v}{\diff t} \diff x &=& \int ( - kx -\mu' mg ) \diff x \\
\\
\int m \frac{\diff v}{\diff t} v \diff t &=& \int ( - kx -\mu' mg) \diff x \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t &=& \int (- kx) \diff x + \int (-\mu' mg) \diff x
\end{eqnarray*}
となる。

　ここで物体から手を放したした時刻を$t=0$とし、初期条件を$v(0) = v_0 =0 ,\ v(t) = v ,\ x(0) = -L ,\ x(t) = x$とすると

\begin{eqnarray*}
\int \frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t &=& \int (- kx) \diff x + \int (-\mu' mg) \diff x \\
\\
\left[ \frac{1}{2} mv^2(t) \right]_{0}^{t} &=& \left[-\frac{1}{2}k x^2 \right]_{-L}^{x} + \left[-\mu' mg x \right]_{-L}^{x} \\
\\
\frac{1}{2} mv^2(t) - \frac{1}{2} mv^2(0) &=& -\frac{1}{2}k x^2 - \left[-\frac{1}{2}k (-L)^2 \right] + (-\mu' mg x)- \left[-\mu' mg (-L) \right] \\
\\
\frac{1}{2} mv^2 - \frac{1}{2}m \cdot 0^2 &=& -\frac{1}{2}k x^2 + \frac{1}{2}k L^2 + \left[ - \mu' mg (x+L) \right] \\
\\
\frac{1}{2} mv^2 +\frac{1}{2}k x^2 &=&\frac{1}{2}k L^2 + \left[ - \mu' mg (x+L) \right]
\end{eqnarray*}
となる。

　時刻を$t_2$でバネと物体が離れたとすると、離れた瞬間の速度$v_2$は

\begin{eqnarray*}
\frac{1}{2} mv_2^2 +\frac{1}{2}k \cdot 0^2 &=&\frac{1}{2}k L^2 + \left[ - \mu' mg (0+L) \right] \\
\\
\frac{1}{2} mv_2^2 &=& \frac{1}{2}k L^2 - \mu' mg L \\
\\
v_2^2 &=& \frac{k}{m}L^2 - 2 \mu' gL \\
\\
v_2 &=& \sqrt{\frac{k}{m}L^2 - 2 \mu' gL}
\end{eqnarray*}
となる。

教科書的計算 ~ 水平面が滑らかなで摩擦がない場合

　エネルギー保存則より

\begin{eqnarray*}
\frac{1}{2} mv^2 +\frac{1}{2}k x^2 &=&\frac{1}{2}k L^2
\end{eqnarray*}

　時刻を$t_1$でバネと物体が離れたとすると、離れた瞬間の速度$v_1$は

\begin{eqnarray*}
\frac{1}{2} mv_1^2 +\frac{1}{2}k \cdot 0^2 &=&\frac{1}{2}k L^2 \\
\\
v_1^2 &=& \frac{k}{m}L^2 \\
\\
v_1 &=& \sqrt{\frac{k}{m}} L
\end{eqnarray*}
となる。

教科書的計算 ~ 水平面が荒く摩擦が作用する場合

　力学的エネルギーの変化が仕事になるので

\begin{eqnarray*}
E(t)-E(0) &=& W(t) \\
\\
\left( \frac{1}{2} mv^2 + \frac{1}{2}k x^2 \right) - \left( \frac{1}{2} m \cdot 0^2 + \frac{1}{2}k L^2 \right) &=& - \mu' mg (x+L) \\
\\
\frac{1}{2} mv^2 + \frac{1}{2}k x^2 - \frac{1}{2}k L^2 &=& - \mu' mg (x+L)
\end{eqnarray*}

　時刻を$t_2$でバネと物体が離れたとすると、離れた瞬間の速度$v_2$は

\begin{eqnarray*}
\frac{1}{2} mv_2^2 + \frac{1}{2}k x^2 - \frac{1}{2}k L^2 &=& - \mu' mg (x+L) \\
\\
\frac{1}{2} mv_2^2 + \frac{1}{2}k \cdot 0^2 - \frac{1}{2}k L^2 &=& - \mu' mg (0+L) \\
\\
\frac{1}{2} mv_2^2 &=& \frac{1}{2}k L^2 - \mu' mg L \\
\\
v_2^2 &=& \frac{k}{m}L^2 - 2 \mu' gL \\
\\
v_2 &=& \sqrt{\frac{k}{m}L^2 - 2 \mu' gL}
\end{eqnarray*}

となる。