仕事とエネルギー ~ 練習問題 part-8
斜面を滑り降りる物体の速度
なめらかな斜面となめらかな水平面が下図のようにつながっている。斜面と水平面のなす角は$\theta$である。物体は点$\text{A}$から斜面を下り、点$\text{B}$を通過し、点$\text{C}$まで達した。点$\text{C}$の通過速度$v_\text{C}$を求めよ。
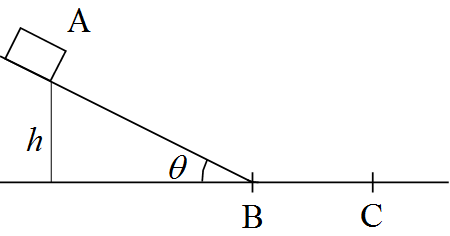
解答
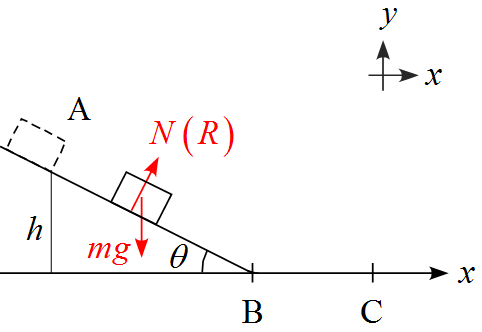
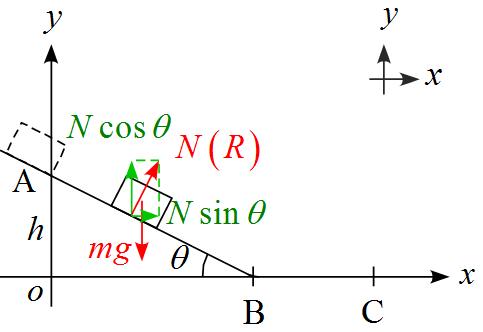
軸を設定し、作用する力を書き込む
- $x$軸の正の向きは右側に、$y$軸の正の向きは上に設定した。
- 作用する力は重力$mg , \ $接触面からの効力$R \ $の2つである。
$x,y$軸に沿った成分に分解すると
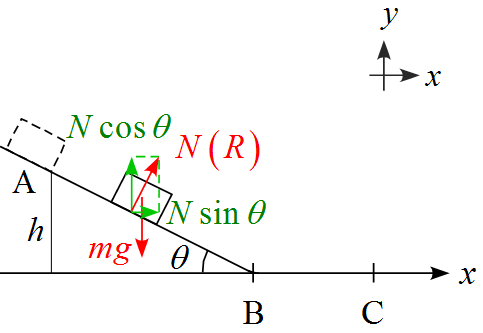
運動方程式は
\begin{eqnarray*}
m a_x &=& N \sin \theta \\
\\
m a_y &=& N \cos \theta - mg
\end{eqnarray*}
となる。
ここで、運動方程式をベクトル表記に書き換えると、
\begin{eqnarray*}
m \vec{a} &=& \vec{F} \\
\\ m
\begin{pmatrix}
a_x \\
a_y \\
\end{pmatrix} &=&
\begin{pmatrix}
F_x \\
F_y \\
\end{pmatrix}\\
\\ m
\begin{pmatrix}
a_x \\
a_y \\
\end{pmatrix} &=&
\begin{pmatrix}
N \sin \theta \\
N \cos \theta - mg \\
\end{pmatrix}
\end{eqnarray*}
となる。
仕事を計算する ~ 両辺を$\diff \vec{r}$で積分する
両辺を$\diff \vec{r}$の内積を取って全体を積分すると
\begin{eqnarray*}
m \vec{a} &=& \vec{F} \\
\\
\int m\frac{\diff \vec{v}}{\diff t} \cdot \diff \vec{r} &=& \int \vec{F} \cdot \diff \vec{r} \\
\\
\int m\frac{\diff \vec{v}}{\diff t} \cdot \vec{v} \diff t &=& \int \vec{F} \cdot \diff \vec{r} \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t &=& \int \vec{F} \cdot \diff \vec{r} \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t
&=& \int
\begin{pmatrix}
F_x \\
F_y \\
\end{pmatrix} \cdot
\begin{pmatrix}
\diff x \\
\diff y \\
\end{pmatrix} \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t
&=& \int F_x \diff x + \int F_y \diff y \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t
&=& \int (N \sin \theta) \diff x + \int (N \cos \theta - mg) \diff y \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t
&=& \int (N \sin \theta) \diff x + \int N \cos \theta \diff y + \int (-mg) \diff y
\end{eqnarray*}
となる。

ここで、変位$\diff \vec{r}$の位置関係は下図のようになる。
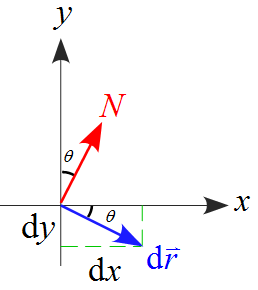
よって、
\begin{eqnarray*}
\tan \theta &=& \frac{-\diff y}{\diff x} \\
\\
\diff x &=& \frac{-\diff y}{\tan \theta}
\end{eqnarray*}
であるから、垂直抗力$N$のする仕事は
\begin{eqnarray*}
W_N &=& W_{N_x} +W_{N_y} \\
\\
&=& \int N \sin \theta \diff x + \int N \cos \theta \diff y \\
\\
&=& \int N \sin \theta \cdot \frac{-\diff y}{\tan \theta} + \int N \cos \theta \diff y \\
\\
&=& \int N \sin \theta \cdot \frac{ \cos \theta}{\sin \theta}\ (-\diff y)+ \int N \cos \theta \diff y \\
\\
&=& \int (-N \cos \theta) \diff y +\int N \cos \theta \diff y \\
\\
&=& 0
\end{eqnarray*}
となる。
つまり、垂直抗力$N$については、垂直抗力$\vec{N}$と変位$\diff \vec{r}$のなす角は常に$90^{\circ}$であるから仕事はしないという事が確認できたことになる。
従って、仕事とエネルギーの関係式は
\begin{eqnarray*}
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t
&=& \int N \sin \theta \diff x + \int N \cos \theta \diff y + \int (-mg) \diff y \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t &=& \int (-mg) \diff y
\end{eqnarray*}
となる。
ここで初期条件は$v(0) = v_0 =0 ,\ x(0) = 0 ,\ y(0) = h $とすると
点$\text{B}$に達する時刻を$t_{\text{B}}$とすると
\begin{eqnarray*}
\int_{0}^{t_{\text{B}}} \frac{\diff}{\diff t} \left( \frac{1}{2}mv^2 \right) \diff t &=& \int_{h}^{0} (-mg) \diff y \\
\\
\left[ \frac{1}{2}mv^2(t) \right]_{0}^{t_{\text{B}}} &=& \left[ -mgx \right]_{h}^{0} \\
\\
\frac{1}{2}mv^2(t_{\text{B}}) -\frac{1}{2}mv^2(0) &=& -mg \cdot 0 - [ -mg \cdot h ] \\
\\
\frac{1}{2}mv^2(t_{\text{B}}) -\frac{1}{2}m \cdot 0^2 &=& mgh\\
\\
\frac{1}{2}mv^2(t_{\text{B}}) &=& mgh
\end{eqnarray*}
となる。
この式が所謂、エネルギー保存則を表した式である。

斜面の切れ目の瞬間の速度$v_{\text{B}}$は
\begin{eqnarray*}
\frac{1}{2}mv^2(t_{\text{B}}) &=& mgh \\
\\
v_{\text{B}}^2 &=& 2gh \\
\\
v_{\text{B}} &=& \sqrt{2gh}
\end{eqnarray*}
となる。
斜面と水平面は滑らかに接続されているので、$v_{\text{B}}$の大きさのまま$v_{\text{C}}$となる。
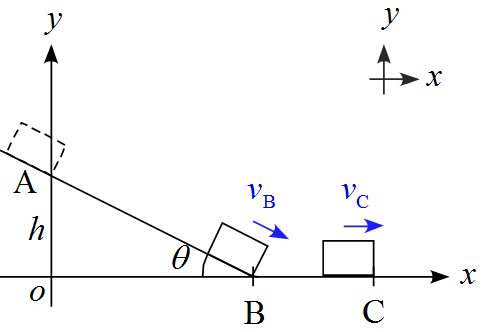
教科書的計算
エネルギー保存則より
\begin{eqnarray*}
\frac{1}{2}mv^2(t_{\text{B}}) &=& mgh
\end{eqnarray*}
斜面の切れ目の瞬間の速度$v_{\text{B}}$は
\begin{eqnarray*}
\frac{1}{2}mv^2(t_{\text{B}}) &=& mgh \\
\\
v_{\text{B}}^2 &=& 2gh \\
\\
v_{\text{B}} &=& \sqrt{2gh}
\end{eqnarray*}
となる。
斜面と水平面は滑らかに接続されているので、$v_{\text{B}}$の大きさのまま$v_{\text{C}}$となる。