仕事とエネルギー ~ 練習問題 part-5
バネに取り付けられた物体の運動
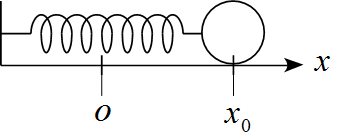
下図のようにバネの一端が壁に固定され、他端に質量$m$の物体が取り付けられている。この物体を自然長から$x_0$だけ伸ばした後、静かに放したところ物体が運動を始めた。この運動での仕事とエネルギーについて検討せよ。但し、物体はなめらかな水平面上にあり、またバネの質量は無視できるものとする。
解答
軸を設定し、作用する力を書き込む
- $x$軸の正の向きは右側に、$y$軸の正の向きは上に設定した。
- バネの自然長の位置を原点とした。
- 作用する力は重力$mg , \ $面からの抗力$N(R) ,\ $バネの復元力$F$の3つである。
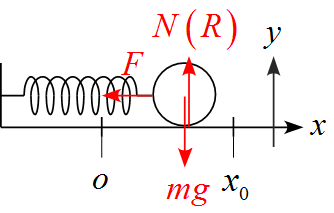
運動方程式を立てる
運動方程式は
\begin{eqnarray*}
m a_x &=& -F \\
\\
m a_y &=& N - mg
\end{eqnarray*}
となる。
となる。
束縛条件より$a_y=0$であるから
\begin{eqnarray*}
ma_x &=& - F \\
\\
0 &=& N - mg
\end{eqnarray*}
となる。
ここで、バネの復元力の大きさ$F$はバネ定数$k$とするとフックの法則$F =kx$となる。
仕事を計算する ~ 両辺を$x$で積分する
$x$軸の運動に着目するので$a_x = a$と書き換えて両辺を$x$で積分すると
\begin{eqnarray*}
ma &=& - kx \\
\\
m \frac{\diff v}{\diff t} &=& - kx \\
\\
\int m \frac{\diff v}{\diff t} \diff x &=& \int ( - kx) \diff x \\
\\
\int m \frac{\diff v}{\diff t} v \diff t &=& \int ( - kx) \diff x \\
\\
\int \frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t &=& \int (- kx) \diff x
\end{eqnarray*}
となる。

ここで物体から手を放したした時刻を$t=0$とし、初期条件を$v(0) = v_0 =0 ,\ v(t) = v ,\ x(0) = x_0 ,\ x(t) = x$とすると
\begin{eqnarray*}
\int \frac{\diff}{\diff t} \left( \frac{1}{2} mv^2 \right) \diff t &=& \int (- kx) \diff x \\
\\
\left[ \frac{1}{2} mv^2(t) \right]_{0}^{t} &=& [-\frac{1}{2}k x^2]_{x_0}^{x} \\
\\
\frac{1}{2} mv^2(t) - \frac{1}{2} mv^2(0) &=& -\frac{1}{2}k x^2 - (-\frac{1}{2}k x_0^2) \\
\\
\frac{1}{2} mv^2 - \frac{1}{2}m \cdot 0^2 &=&-\frac{1}{2}k x^2 - (-\frac{1}{2}k x_0^2) \\
\\
\frac{1}{2} mv^2 +\frac{1}{2}k x^2 &=&\frac{1}{2}k x_0^2
\end{eqnarray*}
となる。
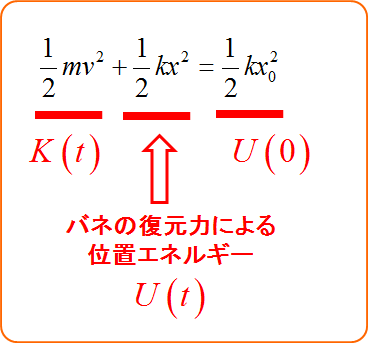
教科書的計算

運動方程式は
\begin{eqnarray*}
m a_x &=& -F \\
\\
m a_y &=& N - mg
\end{eqnarray*}
となる。
となる。
束縛条件より$a_y=0$であるから
\begin{eqnarray*}
ma_x &=& - F \\
\\
0 &=& N - mg
\end{eqnarray*}
となる。
ここで、バネの復元力の大きさ$F$はバネ定数$k$とするとフックの法則$F =kx$となる。
従って、運動方程式は$a_x=a$と書き直すと
\begin{eqnarray*}
ma &=& - kx
\end{eqnarray*}
となる。
この運動は$a=\displaystyle -\frac{k}{m} x \neq \text{const.}$であり、等加速度運動ではない。
従って、等加速度運動の速度と距離の関係式が利用できない。
ここで、仕事の定義を振り返ると下図のような微小区間の微小仕事$\Delta W$は
\begin{eqnarray*}
\Delta W = kx' \cdot \Delta x'
\end{eqnarray*}
である。
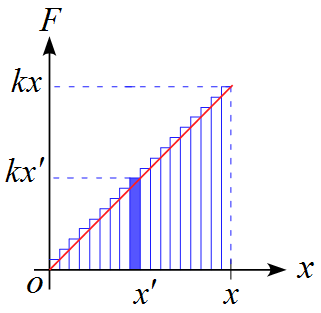
従って、全区間$0 \to x$までの和は
\begin{eqnarray*}
W &=& kx \cdot x \\
\\
&=& \frac{1}{2}kx^2
\end{eqnarray*}
となる。