力のモーメントと運動方程式
力のモーメントについて運動方程式から考えてみよう。数学としてはベクトルの外積を使うので、少し高校の範囲を超えるが、流れを理解しておくことは大事である。
力のモーメントの例題
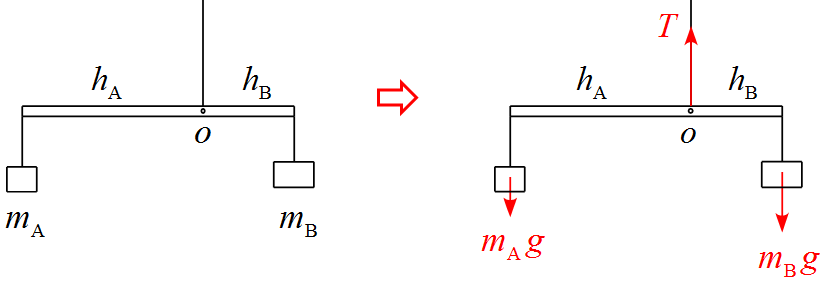
下図のように軽い棒に2つの物体$\text{A,B}$が取り付けられているモデルを見たことがあるだろう。点$\text{O}$を支点としてつり合う条件を考える問題などは有名である。
\begin{eqnarray*}
\text{反時計回りの力のモーメント} &=& h_A m_A g \\
\\
\text{時計回りの力のモーメント} &=& h_B m_B g \\
\end{eqnarray*}
反時計回りの力モーメントと時計回りの力のモーメントが等しくなれば回転しないことになる。この力のモーメントについて運動方程式から考えてみよう。
運動方程式に左から位置ベクトルの$\vec{r}$の外積をとる
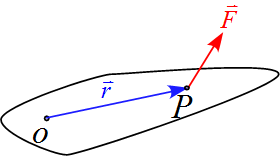
一般的な運動モデルを設定する。原点を$\text{O}$として点$\text{P}$の位置に力$\vec{F}$が作用したと考える。このときの点$\text{P}$の位置ベクトルを$\vec{r}$とする。
運動方程式
\begin{eqnarray*}
m\vec{a}=\vec{F} \\
\\
m\frac{\diff \vec{v}}{\diff t}=\vec{F}
\end{eqnarray*}
の両辺に左側から位置ベクトル$\vec{r}$の外積をとると
\begin{eqnarray*}
\vec{r} \times m\frac{\diff \vec{v}}{\diff t} &=&\vec{r} \times \vec{F} \\
\\
\frac{\diff}{\diff t}(\vec{r} \times m \vec{v}) &=& \vec{r} \times \vec{F} \ \cdots (*) \\
\\
\end{eqnarray*}
と変形できる。この式の左辺の微分括弧内の部分$\vec{r} \times m \vec{v}$を「角運動量$\vec{L}$」と呼び、右辺の$\vec{r} \times \vec{F}$を「力のモーメント$\vec{M}$」と呼ぶ。
即ち、運動方程式の両辺に左側から位置ベクトル$\vec{r}$の外積をとると「力のモーメントと角運動量の関係」が導かれることになる。

- 角運動量$\vec{L}$はベクトル量である。
- 力のモーメント$\vec{M}$はベクトル量である。
式$(*)$の左辺の変形について
実際に左辺を計算してみると
\begin{eqnarray*}
\frac{\diff}{\diff t}(\vec{r} \times m \vec{v}) &=& \frac{\diff \vec{r}}{\diff t} \times m \vec{v} + \vec{r} \times \frac{\diff}{\diff t}(m \vec{v}) \\
\\
&=& \vec{v} \times m \vec{v} + \vec{r} \times \frac{\diff}{\diff t}(m \vec{v}) \\
\\
&=& 0 + \vec{r} \times \frac{\diff}{\diff t}(m \vec{v}) \\
\\
&=& \vec{r} \times m \frac{\diff \vec{v}}{\diff t} \\
\end{eqnarray*}
となり、式変形する前の形になることが確認できる。
回転の運動方程式
式$(*)$を角運動量$\vec{L}$と力のモーメント$\vec{M}$を使って表すと
\begin{eqnarray*}
\frac{\diff \vec{L}}{\diff t} =\vec{M}
\end{eqnarray*}
となり、これを「回転の運動方程式」と呼ぶ。
