相対速度
特に断りがない場合は観測者は静止している前提で考える。しかし、観測者が動いている場合、観測者から見た観測対象の速度を「相対速度」と呼ぶ。
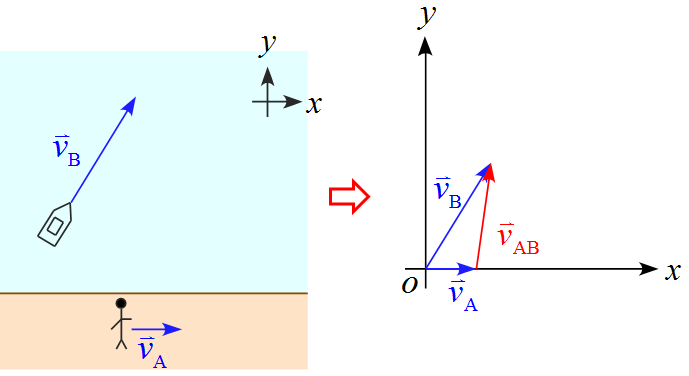
相対速度$\vec{v}_{\text{AB}}$は「$\text{A}$から見た$\text{B}$の相対速度」或いは、「$\text{A}$に対する$\text{B}$の相対速度」となる。
\begin{eqnarray*}
\vec{v}_{\text{AB}} &=& \vec{v}_{\text{B}} - \vec{v}_{\text{A}}
\end{eqnarray*}
観測者が岸を歩いている人とすると、歩いている人から見た船の速度が相対速度$\vec{v}_{\text{AB}}$となる。
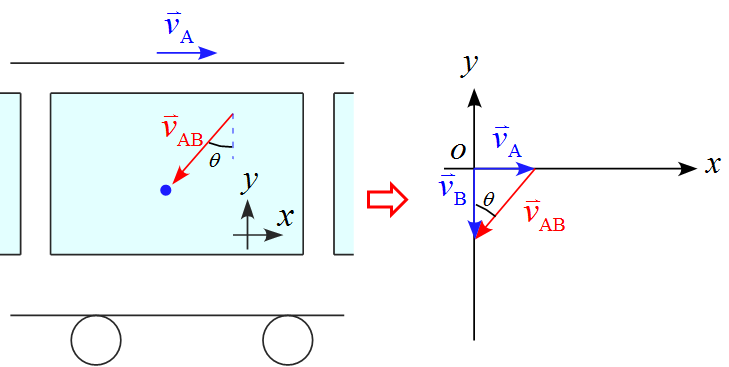
車窓から見た雨滴の相対速度
電車の速度を$\vec{v}_{\text{A}}$とし雨滴の速度を$ \vec{v}_{\text{B}}$とした時、電車内から見た雨滴の相対速度$ \vec{v}_{\text{AB}}$は下図のように作図ができる。
\begin{eqnarray*}
\vec{v}_{\text{AB}} &=& \vec{v}_{\text{B}} - \vec{v}_{\text{A}} \\
\\
\vec{v}_{\text{A}} + \vec{v}_{\text{AB}} &=& \vec{v}_{\text{B}}
\end{eqnarray*}
となる。ベクトルの和の形で式を見たほうが解りやすいかもしれない。
鉛直方向に対してなす角を$\theta$とすると、
\begin{eqnarray*}
\tan \theta = \frac{\vec{v}_{\text{A}}}{\vec{v}_{\text{B}}}
\end{eqnarray*}
より、雨滴の速度$\vec{v}_{\text{B}}$は
\begin{eqnarray*}
\vec{v}_{\text{B}} = \frac{\vec{v}_{\text{A}}}{\tan \theta}
\end{eqnarray*}
と表される。