速度・速さ ~ 練習問題 part-1
今回は速度に関連した基礎的な練習問題を取り上げる。速度の定義をもとに考える流れを解説していく。
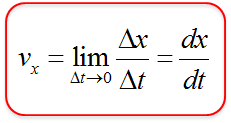
速度・速さ ~ 練習問題 part-1
速さ ~ 時速($\mbox{km/h}$)・分速($\mbox{m/s}$)
A地点を出発した車が$90\ \mbox{s}$後に$1.5\ \mbox{km}$離れたB地点に到着した。このときの平均の速さ$\bar{v}$を時速($\mbox{km/h}$)と分速($\mbox{m/s}$)で表わせ。
- $\Delta t =90\ \mbox{s}$
- $\Delta x =1.5\ \mbox{km}$
速度の定義$v=\displaystyle \frac{\diff x}{\diff t}$より
\begin{eqnarray*}
\bar{v} &=& \frac{\Delta x}{\Delta t} \\
\\
&=& \frac{1.5\ \times 10^{3}\ \mbox{m}}{90\ \mbox{s}} \\
\\
&=& \frac{50}{3}\ \mbox{m/s}\\
\\
&=& 16.66 \ \mbox{m/s}\\
\\
&=& 17\ \mbox{m/s}
\end{eqnarray*}
また、時速($\mbox{km/h}$)で表すと、
\begin{eqnarray*}
\bar{v} &=& \frac{50}{3}\ \mbox{m/s}\\
\\
&=& \frac{50}{3} \times 10^{-3} \times 60 \times 60 \ \mbox{km/h}\\
\\
&=& 60\ \mbox{km/h}\\
\end{eqnarray*}
となる。
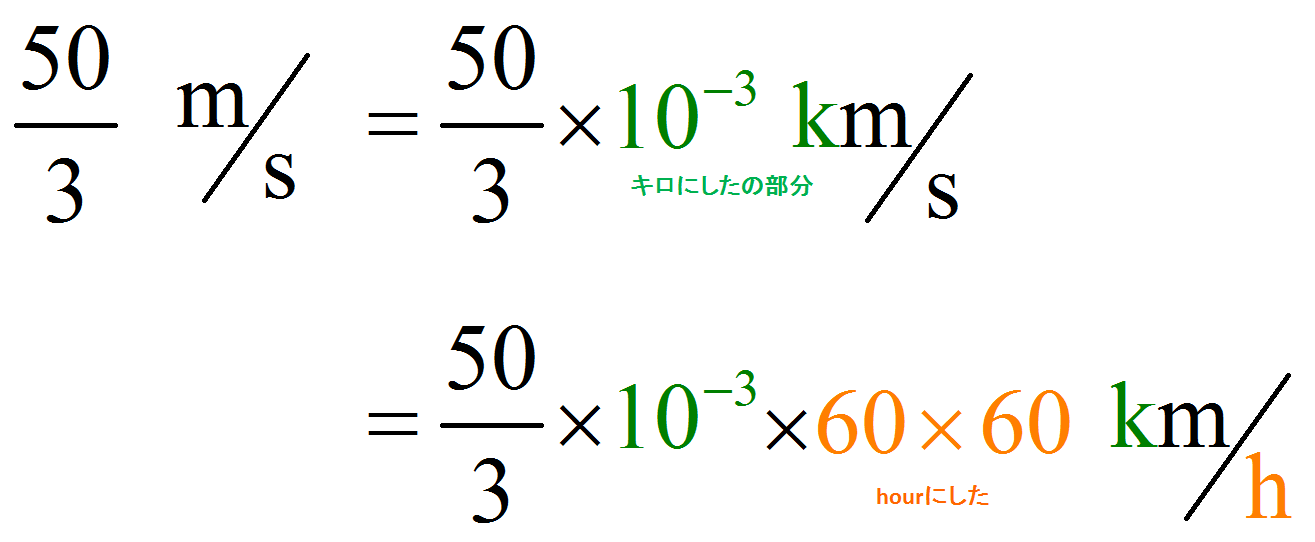
- 問題文から条件を正しく読み解くこと。書き出すと尚良い。
- 与えられた数値は有効数字2桁なので、結果も有効数字2桁で答える。
- 単位の変換は単に暗記するのではなく、式変形から導かれることを理解する。
- 速度の定義$v=\displaystyle \frac{\diff x}{\diff t}$をもとに、条件をあてはめて行く流れである。
$v-t$グラフ・$x-t$グラフ
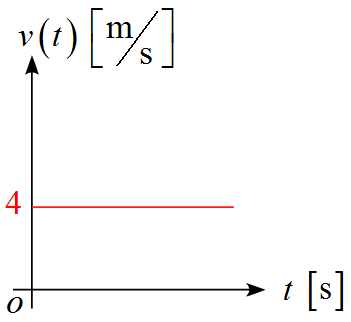
時刻$t=0\ \mbox{s}$で原点にあった物体が、速度$4\ \mbox{m/s}$で$x$軸上を等速度運動している。$v-t$グラフと$x-t$グラフで表わせ。
- $\displaystyle \frac{\diff x}{\diff t} =4\ \mbox{m/s}$
- $x(0)=0$

- 問題文から条件を正しく読み解くこと。書き出すと尚良い。
- 速度$v=\displaystyle \frac{\diff x}{\diff t}$は一定値である。つまり、$x-t$グラフの傾きが一定であることを意味している。
- 速度$v=\displaystyle \frac{\diff x}{\diff t}$は一定値である。つまり、$v-t$グラフは常に一定の値であることを意味している。
速度と変位
物体が一定の速度$1.5 \mbox{m/s}$で運動中のとき、$15$秒間に移動する距離は何$\mbox{m}$か答えよ。
- $\frac{\diff x}{\diff t} =1.5\ \mbox{m/s}$
- $x(15)=$? $\ \mbox{m}$
速度の定義$v=\displaystyle \frac{\diff x}{\diff t}$より
\begin{eqnarray*}
\bar{v} &=& \frac{\Delta x}{\Delta t} \\
\\
\Delta x &=& \bar{v} \cdot \Delta t \\
\\
&=& 1.5\ \mbox{m/s} \times 15\ \mbox{s}\\
\\
&=& 22.5\ \mbox{m}\\
\\
&=& 23\ \mbox{m}
\end{eqnarray*}
となる。
- 問題文から条件を正しく読み解くこと。書き出すと尚良い。
- 速度の定義$v=\displaystyle \frac{\diff x}{\diff t}$をもとに、条件をあてはめて行く流れである。
- 与えられた数値は有効数字2桁なので、結果も有効数字2桁で答える。